編輯:關於android開發

1.具體算法
/**
* 算法3.2 二分查找(基於有序數組)
* Created by huazhou on 2015/11/29.
*/
public class BinarySearchST<Key extends Comparable<key>, Value> {
private Key[] keys;
private Value[] vals;
private int N;
public BinarySearchST(int capacity){
keys = (Key[])new Comparable[capacity];
vals = (Value[])new Object[capacity];
}
public int size(){
return N;
}
public boolean isEmpty() {
return size() == 0;
}
public Value get(Key key){
if(isEmpty()){
return null;
}
int i = rank(key);
if(i < N && keys[i].compareTo(key) == 0){
return vals[i];
}
else{
return null;
}
}
public int rank(Key key){
int lo = 0, hi = N-1;
while (lo <= hi) {
int mid = lo + (hi - lo) / 2;
int cmp = key.compareTo(keys[mid]);
if (cmp < 0) hi = mid - 1;
else if (cmp > 0) lo = mid + 1;
else return mid;
}
return lo;
}
//查找鍵,找到則更新值,否則創建新的元素
public void put(Key key, Value val){
int i = rank(key);
if(i < N && keys[i].compareTo(key) == 0){
vals[i] = val;
return;
}
for (int j = N; j > i; j--){
keys[j] = keys[j-1];
vals[j] = vals[j-1];
}
keys[i] = key;
vals[i] = val;
N++;
}
public void delete(Key key){
if (isEmpty()) return;
// compute rank
int i = rank(key);
// key not in table
if (i == N || keys[i].compareTo(key) != 0) {
return;
}
for (int j = i; j < N-1; j++) {
keys[j] = keys[j+1];
vals[j] = vals[j+1];
}
N--;
keys[N] = null; // to avoid loitering
vals[N] = null;
// resize if 1/4 full
if (N > 0 && N == keys.length/4) resize(keys.length/2);
}
}
這段符號表的實現用兩個數組來保存鍵和值。和基於數組的棧一樣,put()方法會在插入新元素前將所有較大的鍵向後移動一格。
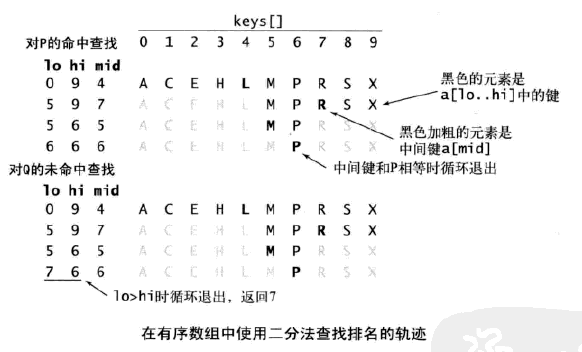
rank()方法實現了正文所述的經典算法來計算小於給定鍵的鍵的數量。它首先將key和中間鍵比較,如果相等則返回其索引;如果小於中間鍵則在左半部分查找;大於則在右半部分查找。
public Key min(){
return keys[0];
}
public Key max(){
return keys[N-1];
}
public Key select(int k){
return keys[k];
}
public Key ceiling(Key key){
int i = rank(key);
return keys[i];
}
public Key floor(Key key){
int i = rank(key);
if (i < N && key.compareTo(keys[i]) == 0) return keys[i];
if (i == 0) return null;
else return keys[i-1];
}
public boolean contains(Key key) {
return get(key) != null;
}
public Iterable<Key> keys(Key lo, Key hi){
Queue<Key> q = new Queue<Key>();
for (int i = rank(lo); i < rank(hi); i++){
q.enqueue(keys[i]);
}
if(contains(hi)){
q.enqueue(keys[rank(hi)]);
}
return q;
}
2.算法分析
rank()的遞歸實現還能夠讓我們立即得到一個結論:二分查找很快,因為遞歸關系可以說明算法所需比較次數的上界。
命題:在N個鍵的有序數組中進行二分查找最多需要(lgN+1)次比較(無論是否成功)。
證明:這裡的分析和對歸並排序的分析類似(但相對簡單)。令C(N)為在大小為N的符號表中查找一個鍵所需進行的比較次數。顯然我們有C(0)=0,C(1)=1,且對於N>0我們可以寫出一個和遞歸方法直接對應的歸納關系式:
C(N)<=C(└N/2┘)+1
無論查找會在中間元素的左側還是右側繼續,子數組的大小都不會超過└N/2┘,我們需要一次比較來檢查中間元素和被查找的鍵是否相等,並決定繼續查找左側還是右側的子數組。當N為2的冪減1時(N=2n-1),這種遞推很容易。首先,因為└N/2┘=2n-1-1,所以我們有:
C(2n-1)<=C(2n-1-1)+1
用這個公式代換不等式右邊的第一項可得:
C(2n-1)<=C(2n-2-1)+1+1
將上面這一步重復n-2次可得:
C(2n-1)<=C(20)+n
最後的結果即:
C(N)=C(2n)<=n+1<lgN+1
對於一般的N,確切的結論更加復雜,但不難通過以上論證推廣得到。二分查找所需時間必然在對數范圍之內。

盡管能夠保證查找所需的時間是對數級別的,BinarySearchST仍然無法支持我們用類似FrequencyCounter的程序來處理大型問題,因為put()方法還是太慢了。二分查找減少了比較的次數但無法減少運行所需時間,因為它無法改變以下事實:
在鍵是隨機排列的情況下,構造一個基於有序數組的符號表所需要訪問數組的次數是數組長度的平方級別(在實際情況下鍵的排列雖然不是隨機的,但仍然很好地符合這個模型)。
命題:向大小為N的有序數組中插入一個新的元素在最壞情況下需要訪問~2N次數組,因此向一個空符號表中插入N個元素在最壞情況下需要訪問~N2次數組。
證明:同上命題。
3.總結
一般情況下二分查找都比順序查找快得多,它也是眾多實際應用程序的最佳選擇。當然,二分查找也不適合很多應用。例如,它無法處理Leipzig Corpora數據庫,因為查找和插入操作是混合進行的,而且符號表也太大了。如我們所強調的那樣,現代應用需要同時能夠支持高效的查找和插入兩種操作的符號表實現。也就是說,我們需要在構造龐大的符號表的同時能夠任意插入(也許還有刪除)鍵值對,同時也要能夠完成查找操作。

【源碼下載】
 RecyclerView的五大開源項目-解決辦法
RecyclerView的五大開源項目-解決辦法
RecyclerView的五大開源項目-解決辦法 前段時間做項目由於采用的MD設計,所以必須要使用RecyclerView全面代替ListView。但是開發中遇到了
 Android 獲取系統的聯系人,android獲取聯系人
Android 獲取系統的聯系人,android獲取聯系人
Android 獲取系統的聯系人,android獲取聯系人本文主要介紹android中怎樣獲取系統的聯系人數據 首先打開模擬器 點擊聯系人圖標按鈕 說明系統聯系人數據
 詳解Android Handler的使用
詳解Android Handler的使用
我們進行Android開發時,Handler可以說是使用非常頻繁的一個概念,它
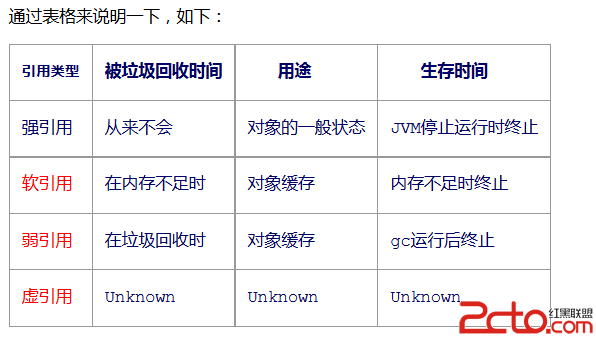 Android 面試題總結(二)
Android 面試題總結(二)
Android 面試題總結(二) 前言 筆者最近離職找工作快兩周了,這段時間陸陸續續也見識了北上廣這邊跟西部城市對待技術理念的差異和學習深度.俗話說:知恥而後勇,在經歷了