編輯:關於android開發
快速排序可能是應用最廣泛的排序算法了。流行的原因是它實現簡單、適用於各種不同的輸入數據且在一般應用中比其他排序算法都要快得多。快速排序引人注目的特點包括它是原地排序(只需要一個很小的輔助棧),且將長度為N的數組排序所需的時間和NlgN成正比。我們已經學習過的排序算法都無法將這兩個優點結合起來。另外,快速排序的內循環比大多數排序算法都要短小,這意味著它無論是在理論上還是在實際中都要更快。
1.基本思想
快速排序是一種分治的排序算法。它將一個數組分成兩個子數組,將兩部分獨立地排序。快速排序和歸並排序是互補的:歸並排序將數組分成兩個子數組分別排序,並將有序的子數組歸並以將整個數組排序;而快速排序將數組排序的方式則是當兩個子數組都有序時整個數組也就自然有序了。在第一種情況中,遞歸調用發生在處理整個數組之前;在第二種情況中,遞歸調用發生在處理整個數組之後。在歸並排序中,一個數組被等分為兩半;在快速排序中,切分的位置取決於數組的內容。如圖

2.具體算法
/**
* 快速排序
* @author huazhou
*
*/
public class Quick extends Model{
public void sort(Comparable[] a){
StdRandom.shuffle(a); //消除對輸入的依賴
sort(a, 0, a.length - 1);
}
private void sort(Comparable[] a, int lo, int hi){
if(hi <= lo){
return ;
}
int j = partition(a, lo, hi); //切分
sort(a, lo, j-1); //將左半部分a[lo..j-1]排序
sort(a, j+1, hi); //將右半部分a[j+1..hi]排序
}
/**
* 快速排序的切分
* 將數組切分為a[lo..i-1],a[i],a[i+1..hi]
*/
private int partition(Comparable[] a, int lo, int hi){
int i = lo, j = hi+1; //左右掃描指針
Comparable v = a[lo]; //切分元素
//掃描左右,檢查掃描是否結束並交換元素
while(true){
while(less(a[++i], v)){
if(i == hi){
break;
}
}
while(less(v, a[--j])){
if(j == lo){
break;
}
}
if(i >= j){
break;
}
exch(a, i, j);
}
exch(a, lo, j); //將v=a[j]放入正確的位置
return j; //a[lo..j-1]<=a[j]<=a[j+1..hi]達成
}
}
快速排序遞歸地將子數組a[lo..hi]排序,先用partition()方法將a[j]放到一個合適位置,然後再用遞歸調用將其他位置的元素排序。

該方法的關鍵在於切分,這個過程使得數組滿足下面三個條件:
■對於某個j,a[j]已經排定;
■a[lo]到a[j-1]中的所有元素都不大於a[j];
■a[j+1]到a[hi]中的所有元素都不小於a[j]。
我們就是通過遞歸地調用切分來排序的。
因為切分過程總是能排定一個元素,用歸納法不難證明遞歸能夠正確地將數組排序:如果左子數組和右子數組都是有序的,那麼由左子數組(有序且沒有任何元素大於切分元素)、切分元素和右子數組(有序且沒有任何元素小於切分元素)組成的結果數組也一定是有序的。
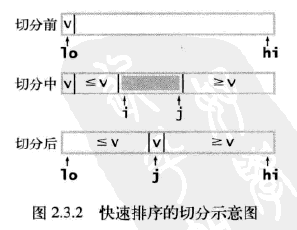
要完成這個實現,需要實現切分方法。一般策略是先隨意地取a[lo]作為切分元素,即那個將會被排定的元素,然後我們從數組的左端開始向右掃描直到找到一個大於等於它的元素,再從數組的右端開始向左掃描直到找到一個小於等於它的元素。這個兩個元素顯然是沒有排定的,因此我們交換它們的位置。如此繼續,我們就可以保證左指針i的左側元素都不大於切分元素,右指針j的右側元素都不小於切分元素。當兩個指針相遇時,我們只需要將切分元素a[lo]和左子數組最右側的元素(a[j])交換然後返回j即可。切分方法的大致過程如下圖。
/**
* 快速排序的切分
* 將數組切分為a[lo..i-1],a[i],a[i+1..hi]
*/
private int partition(Comparable[] a, int lo, int hi){
int i = lo, j = hi+1; //左右掃描指針
Comparable v = a[lo]; //切分元素
//掃描左右,檢查掃描是否結束並交換元素
while(true){
while(less(a[++i], v)){
if(i == hi){
break;
}
}
while(less(v, a[--j])){
if(j == lo){
break;
}
}
if(i >= j){
break;
}
exch(a, i, j);
}
exch(a, lo, j); //將v=a[j]放入正確的位置
return j; //a[lo..j-1]<=a[j]<=a[j+1..hi]達成
}
這段代碼按照a[lo]的值v進行切分。當指針i和j相遇時主循環退出。在循環中,a[i]小於v時我們增大i,a[j]大於v時我們減小j,然後交換a[i]和a[j]來保證i左側的元素都不大於v,j右側的元素都不小於v。當指針相遇時交換a[lo]和a[j],切分結束(這樣切分值就留在a[j]中了)。
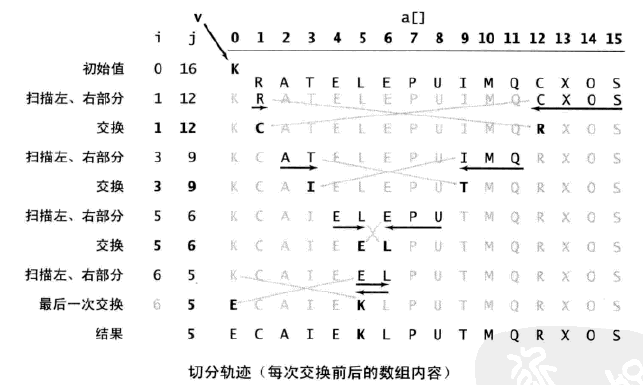
2.1 原地切分
如果使用一個輔助數組,我們可以很容易實現切分,但將切分後的數組復制回去的開銷也許會使我們得不償失。一個初級java程序員甚至可能會將空數組創建在遞歸的切分方法中,這會大大降低排序的速度。
2.2 別越界
如果切分元素是數組中最小或最大的那個元素,我們就要小心別讓掃描指針跑出數組的邊界。partition()實現可進行明確的檢測來預防這種情況。測試條件(j == lo)是冗余的,因為切分元素就是a[lo],它不可能比自己小。數組右端也有相同的情況,它們都是可以去掉的。
2.3 保持隨機性
數組元素的順序是被打亂過的。因為快速排序算法對所有的子數組都一視同仁,它的所有子數組也都是隨機排序的。這對於預測算法的運行時間很重要。保持隨機性的另一種方法是在partition()中隨機選擇一個切分元素。
2.4 終止循環
一個最常見的錯誤是沒有考慮到數組中可能包含和切分元素的值相同的其他元素。
2.5 處理切分元素值有重復的情況
左側掃描最好是在遇到大於等於切分元素值的元素時停下,右側掃描則是遇到小於等於切分元素值的元素時停下。盡管這樣可能會不必要地將一些等值的元素交換,但在某些典型應用中,它能夠避免算法的運行時間變為平方級別。
2.6 終止遞歸
例如,實現快速排序時一個常見的錯誤就是不能保證將切分元素放入正確的位置,從而導致程序在切分元素正好是子數組的最大或是最小元素時陷入了無限的遞歸循環之中。
3.算法分析
命題:將長度為N的無重復數組排序,快速排序平均需要~2NlnN次比較(以及1/6的交換)
證明:令CN為將N個不同元素排序平均所需的比較次數。顯然C0=C1=0,對於N>1,由遞歸程序可以得到以下歸納關系:
CN=N+1+(C0+C1+...+CN-2+CN-1)/N+(CN-1+CN-2+...+C0)/N
第一項是切分的成本(總是N+1),第二項是將左子數組(長度可能是0到N-1)排序的平均成本,第三項是將右子數組(長度和左子數組相同)排序的平均成本。將等式左右兩邊乘以N並整理各項得到:
NCN=N(N+1)+2(C0+C1+...+CN-2+CN-1)
將該等式減去N-1時的相同等式可得:
NCN-(N-1)CN-1=2N+2CN-1
整理等式並將兩邊除以N(N+1)可得:
CN/(N+1)=CN-1/N+2/(N+1)
歸納法推導可得:
CN~2(N+1)(1/3+1/4+...+1/(N+1))
括號內的量是曲線2/x下從3到N的離散近似面積加一,積分得到CN~2NlnN。注意到2NlnN≈1.39NlgN,也就是說平均比較次數只比最好情況多39%
4.總結
盡管快速排序有很多優點,它的基本實現仍有一個潛在的缺點:在切分不平衡時這個程序可能會極為低效。例如,如果第一次從最小的元素切分,第二次從第二小的元素切分,如此這般,每次調用只會移除一個元素。這會導致一個大子數組需要切分很多次。我們要在快速排序前將數組隨機排序的主要原因就是要避免這種情況。它能夠使產生糟糕的切分的可能性降到極低,我們就無需為此擔心了。
總的來說,可以肯定的是對於大小為N的數組,快速排序算法的運行時間在1.39NlgN的某個常數因子的范圍之內。歸並排序也能做到這一點,但是快速排序一般會更快(盡管它的比較次數多39%),因為它移動數據的次數更少。這些保證都來自於數學概率,你完全可以相信它。
千萬級
億級
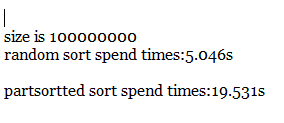
5.算法改進
如果你的排序代碼會被執行很多次或者會被用在大型數組上(特別是如果它會被發布成一個庫函數,排序的對象數組的特性是未知的),那麼下面的改進意見值得你參考。需要注意的是,你需要通過實驗來確定改進的效果並為實現選擇最佳的參數。一般來說它們能將性能提升20%~30%
切換到插入排序
和大多數遞歸排序算法一樣,改進快速排序性能的一個簡單辦法基於以下兩點:
■對於小數組,快速排序比插入排序慢;
■因為遞歸,快速排序的sort()方法在小數組中也會調用自己。
因此,在排序小數組時應該切換到插入排序。簡單地改動算法就可以做到這一點:將sort()中的語句
if(hi <= lo) return;
替換成下面這條語句來對小數組使用插入排序:
if(hi <= lo + M){Insertion.sort(a, lo, hi); return;}
轉換參數M的最佳值是和系統相關的,但是5~15之間的任意值在大多數情況下都能令人滿意。
【源碼下載】
 打造簡易NineoldAndroids動畫庫,深入理解Android動畫原理
打造簡易NineoldAndroids動畫庫,深入理解Android動畫原理
打造簡易NineoldAndroids動畫庫,深入理解Android動畫原理 簡介 NineoldAndroids是Github上一個著名的動畫庫,簡單來說,Nine
 【轉】連接MySQL數據庫(android,php,MySQL),mysqlandroid
【轉】連接MySQL數據庫(android,php,MySQL),mysqlandroid
【轉】連接MySQL數據庫(android,php,MySQL),mysqlandroid管理MySQL數據庫最簡單和最便利的方式是PHP腳本。運行PHP腳本使用HTTP
 Android逆向之旅---解析編譯之後的Resource.arsc文件格式
Android逆向之旅---解析編譯之後的Resource.arsc文件格式
Android逆向之旅---解析編譯之後的Resource.arsc文件格式 一、前言 快過年了,先提前祝賀大家新年快樂,這篇文章也是今年最後一篇了。今天我們繼續來看
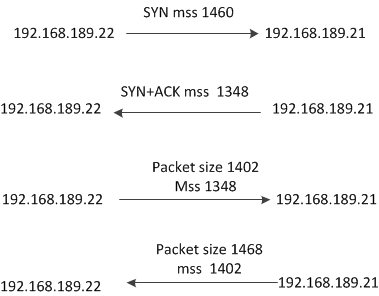 關於TCP MSS的內核設置
關於TCP MSS的內核設置
關於TCP MSS的內核設置下面是一個MSS交互的例子,在三次握手的過程中兩個主機捎帶了不同的MSS值,192.168.189.22接口的MTU值為1500,192.16
 Android開發4: Notification編程基礎、Broadcast的使用及其靜態注冊、動態注冊方式,靜態庫與動態庫編程
Android開發4: Notification編程基礎、Broadcast的使用及其靜態注冊、動態注冊方式,靜態庫與動態庫編程
Android開發4: Notification編程基礎、Broadca