編輯:關於android開發
實現棧或是隊列與實現優先隊列的最大不同在於對性能的要求。對於棧和隊列,我們的實現能夠在常數時間內完成所有操作;而對於優先隊列,插入元素和刪除最大元素這兩個操作之一在最壞情況下需要線性時間來完成。我們接下來要討論的基於數據結構堆的實現能夠保證這兩種操作都能更快地執行。
1.堆的定義
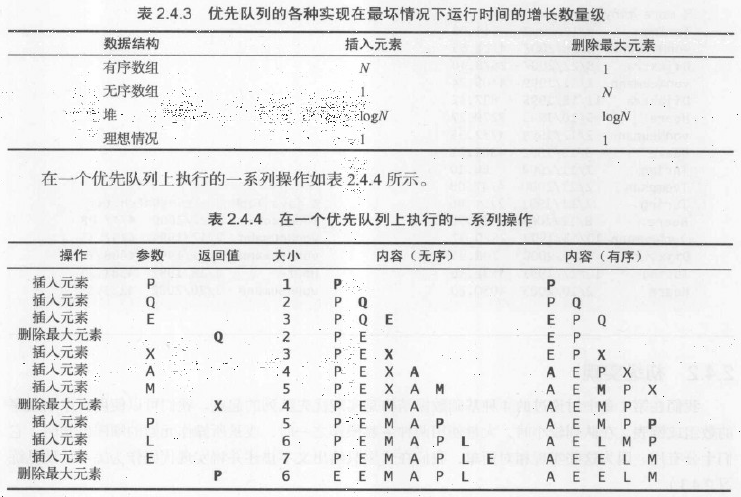
數據結構二叉堆能夠很好地實現優先隊列的基本操作。在二叉堆的數組中,每個元素都要保證大於等於另兩個特定位置的元素。相應地,這些位置的元素又至少要大於等於數組中的另兩個元素,以此類推。如果我們將所有元素畫成一棵二叉樹,將每個較大元素和兩個較小的元素用邊連接就可以很容易看出這種結構。
定義:當一棵二叉樹的每個結點都大於等於它的兩個子結點時,它被稱為堆有序。
相應地,在堆有序的二叉樹中,每個結點都小於等於它的父結點(如果有的話)。從任意結點向上,我們都能得到一列非遞減的元素;從任意結點向下,我們都能得到一列非遞增的元素。
命題:根結點是堆有序的二叉樹中的最大結點
證明:根據樹的性質歸納可得
二叉堆表示法
如果我們用指針來表示堆有序的二叉樹,那麼每個元素都需要三個指針來找到它的上下結點(父結點和兩個子結點各需要一個)。如下圖所示。完全二叉樹只用數組而不需要指針就可以表示。具體方法就是將二叉樹的結點按照層級順序放入數組中,根結點在位置1,它的子結點在位置2和3,而子結點的子結點則分別在位置4、5、6和7,以此類推。
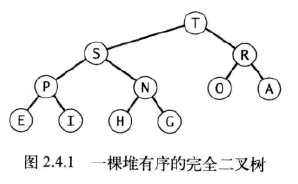
定義:二叉堆是一組能夠用堆有序的完全二叉樹排序的元素,並在數組中按照層級儲存(不使用數組的第一個位置)
簡單起見,在下文中我們將二叉堆簡稱為堆。在一個堆中,位置k的結點的父結點的位置為└k/2┘,而它的兩個子結點的位置則分別為2k和2k+1。這樣在不使用指針的情況下我們也可以通過計算數組的索引在樹中上下移動:從a[k]向上一層就令k等於k/2,向下一層則令k等於2k或2k+1.
用數組(堆)實現的完全二叉樹的結構是很嚴格的,但它的靈活性已經足以讓我們高效地實現優先隊列。用它們我們將能實現對數級別的插入元素和刪除最大元素的操作。利用在數組中無需指針即可沿樹上下移動的便利和以下性質,算法保證了對數復雜度的性能。
命題:一棵大小為N的完全二叉樹的高度為└lgN┘
證明:通過歸納很容易可以證明這一點,且當N達到2的冪時樹的高度會加1
2.堆的算法
堆的操作會首先進行一些簡單的改動,打破堆的狀態,然後再遍歷堆並按照要求將堆的狀態恢復。我們稱這個過程叫做堆的有序化。在有序化的過程中我們會遇到兩種情況。當某個結點的優先級上升(或是在堆底加入一個新的元素)時,我們需要由下至上恢復堆的順序。當某個結點的優先級下降(例如將根結點替換為一個較小的元素)時,我們需要由上至下恢復堆的順序。首先,我們會學習如何實現這兩種輔助操作,然後再用它們實現插入元素和刪除最大元素的操作。
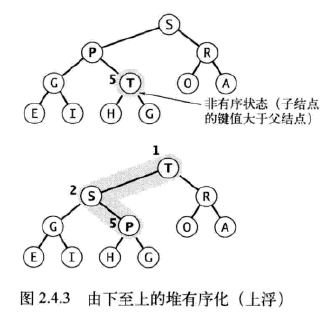
由下至上的堆有序化(上浮)
private void swim(int k) {
while (k > 1 && less(k/2, k)) {
exch(k, k/2);
k = k/2;
}
}
如果堆的有序狀態因為某個結點變得比它的父結點更大而被打破,那麼我們就需要通過交換它和它的父結點來修復堆。交換後,這個結點比它的兩個子結點都大(一個是曾經的父結點,另一個比它更小,因為它是曾經父結點的子結點),但這個結點仍然可能比它現在的父結點更大。我們可以一遍遍地用同樣的辦法恢復秩序,將這個結點不斷向上移動直到我們遇到了一個更大的父結點。只要記住位置k的結點的父結點的位置是└k/2┘,這個過程實現起來很簡單。swim()方法中的循環可以保證只有位置k上的結點大於它的父結點時堆的有序狀態才會被打破。因此只要該結點不再大於它的父結點,堆的有序狀態就恢復了。如下圖
由上至下的堆有序化(下沉)
private void sink(int k) {
while (2*k <= N) {
int j = 2*k;
if (j < N && less(j, j+1)) j++;
if (!less(k, j)) break;
exch(k, j);
k = j;
}
}
如果堆的有序狀態因為某個結點變得比它的兩個子結點或是其中之一更小了而被打破了,那麼我們可以通過將它和它的兩個子結點中的較大者交換來恢復堆。交換可能會在子結點處繼續打破堆的有序狀態,因此我們需要不斷地用相同的方式將其修復,將結點向下移動直到它的子結點都比它更小或是到達了堆的底部。由位置為k的結點的子結點位於2k和2k+1可以直接得到對應的代碼。
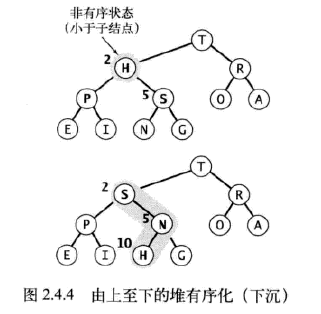
sink()和swim()方法是高效實現優先隊列API的基礎,原因如下。
插入元素。我們將新元素加到數組末尾,增加堆的大小並讓這個新元素上浮到合適的位置(如下圖左半部分所示)。
刪除最大元素。我們從數組頂端刪去最大的元素並將數組的最後一個元素放到頂端,減小堆的大小並讓這個元素下沉到合適的位置(如下圖右半部分所示)。
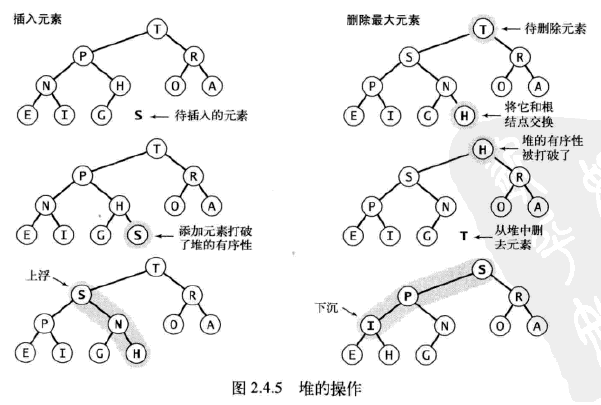
基於堆的優先隊列算法解決了我們在開始時提出的一個基本問題:它對優先隊列API的實現能夠保證插入元素和刪除最大元素這兩個操作的用時和隊列的大小僅成對數關系。
【源碼下載】
 android 網絡_網絡圖片查看器,
android 網絡_網絡圖片查看器,
android 網絡_網絡圖片查看器,xml <?xml version=1.0?> -<LinearLayout tools:context=.Ma
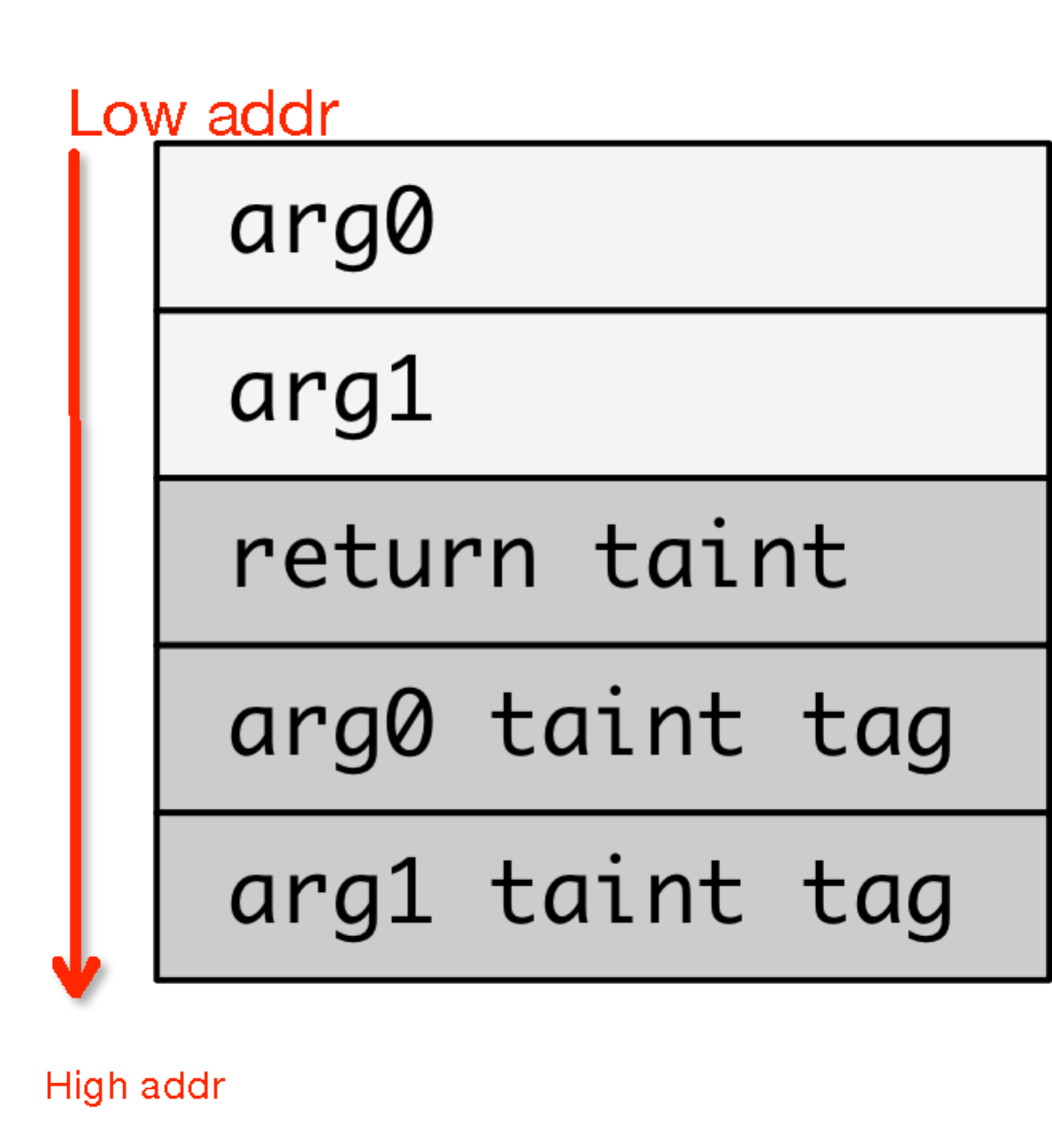 TaintDroid剖析之Native方法級污點跟蹤分析,taintdroidnative
TaintDroid剖析之Native方法級污點跟蹤分析,taintdroidnative
TaintDroid剖析之Native方法級污點跟蹤分析,taintdroidnative1、Native方法的污點傳播 在前兩篇文章中我們詳細分析了TaintDroid
 生動有趣的動畫Toast--第三方開源--NiftyNotification,開源微信第三方平台
生動有趣的動畫Toast--第三方開源--NiftyNotification,開源微信第三方平台
生動有趣的動畫Toast--第三方開源--NiftyNotification,開源微信第三方平台 NiftyNotification在github上的項目主頁是:http
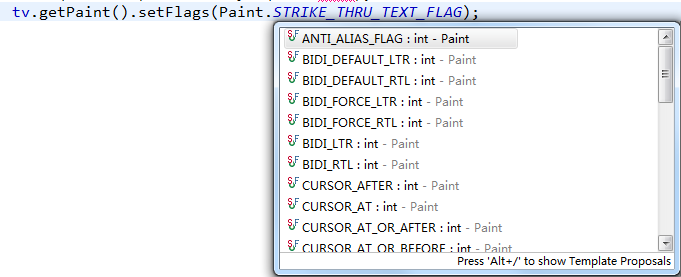 Android中TextView添加刪除線,androidtextview
Android中TextView添加刪除線,androidtextview
Android中TextView添加刪除線,androidtextview項目中的需求~~~~ 商城中物品的一個本身價格,還有一個就是優惠價格。。。需要用到一個刪除線。