編輯:關於android開發
1.具體算法
public class MaxPQ<Key> implements Iterable<Key> {
private Key[] pq; //基於堆的完全二叉樹
private int N; // 存儲於pq[1..N]中,pq[0]沒有使用
private Comparator<Key> comparator; // optional Comparator
public MaxPQ(int initCapacity) {
pq = (Key[]) new Object[initCapacity + 1];
N = 0;
}
/**
* 返回隊列是否為空
*/
public boolean isEmpty() {
return N == 0;
}
/**
* 返回優先隊列中的元素個數
*/
public int size() {
return N;
}
/**
* 返回最大元素
*/
public Key max() {
if (isEmpty()) throw new NoSuchElementException("Priority queue underflow");
return pq[1];
}
/**
* 向優先隊列中插入一個元素
*/
public void insert(Key x) {
// double size of array if necessary
if (N >= pq.length - 1) resize(2 * pq.length);
// add x, and percolate it up to maintain heap invariant
pq[++N] = x;
swim(N);
assert isMaxHeap();
}
/**
* 刪除並返回最大元素
*/
public Key delMax() {
if (isEmpty()) throw new NoSuchElementException("Priority queue underflow");
Key max = pq[1];//從根結點得到最大元素
exch(1, N--); //將其和最後一個結點交換
sink(1); //恢復堆的有序性
pq[N+1] = null; //防止越界
if ((N > 0) && (N == (pq.length - 1) / 4)) resize(pq.length / 2);
assert isMaxHeap();
return max;
}
private void swim(int k) {
while (k > 1 && less(k/2, k)) {
exch(k, k/2);
k = k/2;
}
}
private void sink(int k) {
while (2*k <= N) {
int j = 2*k;
if (j < N && less(j, j+1)) j++;
if (!less(k, j)) break;
exch(k, j);
k = j;
}
}
}
2.算法分析
優先隊列由一個基於堆的完全二叉樹表示,存儲於數組pq[1...N]中,pq[0]沒有使用。在insert()中,我們將N加一並把新元素添加在數組最後,然後用swim()恢復堆的秩序。在delMax()中,我們從pq[1]中得到需要返回的元素,然後將pq[N]移動到pq[1],將N減一並用sink()恢復堆的秩序。同時我們還將不再使用的pq[N+1]設為null,以便系統回收它所占用的空間。
命題:對於一個含有N個元素的基於堆的優先隊列,插入元素操作只需不超過(lgN+1)次比較,刪除最大元素的操作需要不超過2lgN次比較。
證明:由上一個命題可知,兩種操作都需要在根結點和堆底之間移動元素,而路徑的長度不超過lgN。對於路徑上的每個結點,刪除最大元素需要兩次比較(除了堆底元素),一次用來找出較大的子結點,一次用來確定該子結點是否需要上浮。
對於需要大量混雜的插入和刪除最大元素操作的典型應用來說,上面的命題意味著一個重要的性能突破。使用有序或是無序數組的優先隊列的初級實現總是需要線性時間來完成其中一種操作,但基於堆的實現則能夠保證在對數時間內完成它們。這種差別使得我們能夠解決以前無法解決的問題。
堆上的優先隊列操作如下圖
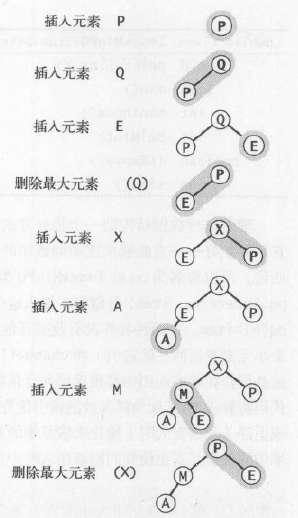
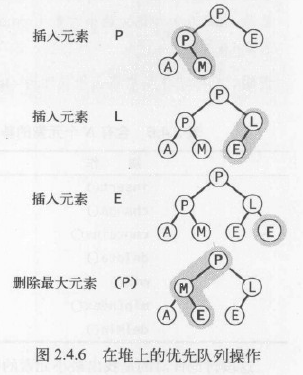
【源碼下載】
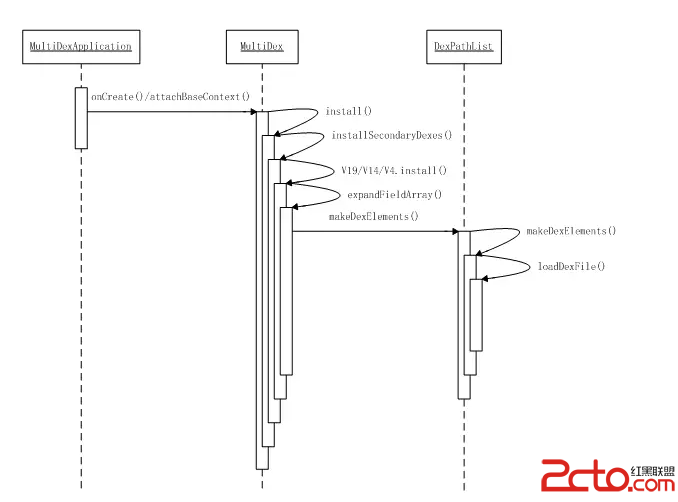 Android插件化(一):使用改進的MultiDex動態加載assets中的apk
Android插件化(一):使用改進的MultiDex動態加載assets中的apk
Android插件化(一):使用改進的MultiDex動態加載assets中的apk 為了解決65535方法數超標的問題,Google推薦使用MultiDex來加載cla
 Android 網絡圖片查看器,
Android 網絡圖片查看器,
Android 網絡圖片查看器,今天來實現一下android下的一款簡單的網絡圖片查看器 界面如下: 代碼如下: <LinearLayout xmlns:and
 單機搭建Android開發環境(五),單機搭建android開發
單機搭建Android開發環境(五),單機搭建android開發
單機搭建Android開發環境(五),單機搭建android開發 前文介紹了Android系統開發環境的搭建,本文將簡單介紹Android應用開發環境的搭建。 基於
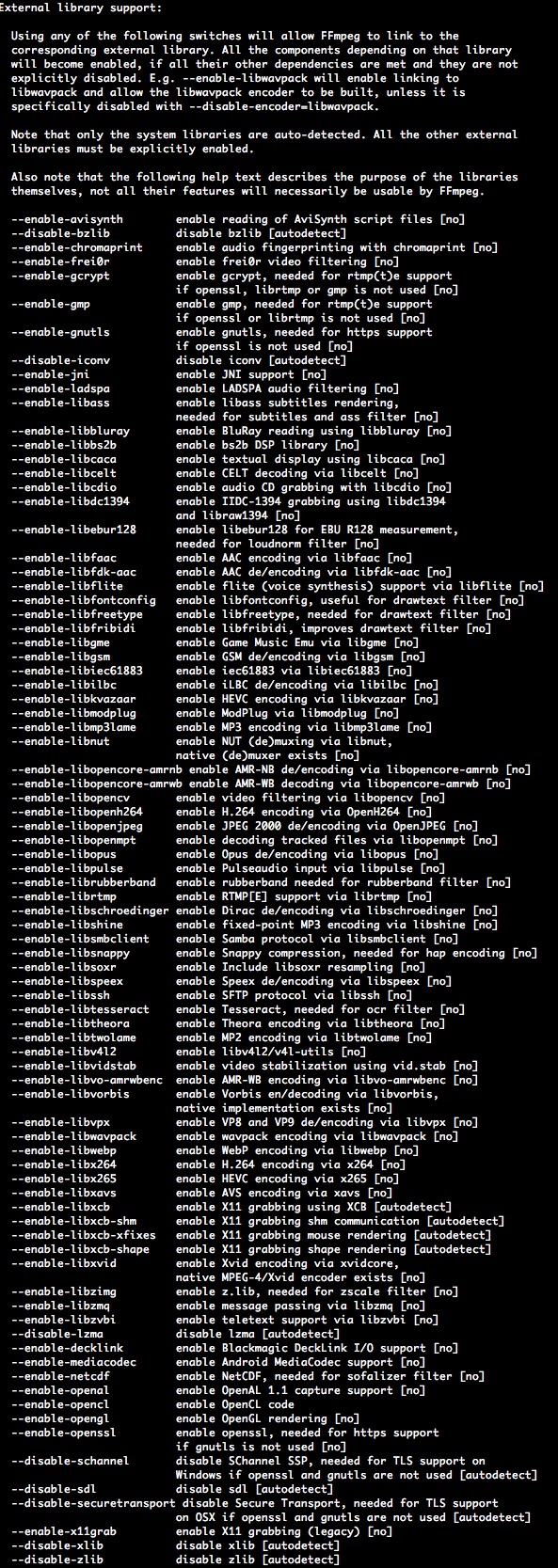 FFmpeg使用手冊 - FFmpeg 編碼支持與定制
FFmpeg使用手冊 - FFmpeg 編碼支持與定制
FFmpeg使用手冊 - FFmpeg 編碼支持與定制3.1 FFmpeg本身支持一些編碼、封裝與協議,但是支持的依然有限,有些是因為licence,有些是因為相對來說比