編輯:關於android開發
1.基本思想
通常人們整理橋牌的方法是一張一張的來,將每一張牌插入到其他已經有序的牌中的適當位置。在計算機的實現中,為了給要插入的元素騰出空間,我們需要將其余所有元素在插入之前都向右移動一位。這種算法叫做插入排序。
與選擇排序一樣,當前索引左邊的所有元素都是有序的,但它們的最終位置還不確定,為了給更小的元素騰出空間,它們可能會被移動。但是當索引到達數組的右端時,數組排序就完成了。
和選擇排序不同的是,插入排序所需的時間取決於輸入中元素的初始順序。例如,對一個很大且其中的元素已經有序(或接近有序)的數組進行排序將會比對隨機順序的數組或是逆序數組進行排序要快得多。
2.具體算法
/**
* 插入排序
* @author huazhou
*
*/
public class Insertion extends Model{
//將a[]按升序排列
public void sort(Comparable[] a){
int N = a.length;
//將a[i]插入到a[i-1]、a[i-2]、a[i-3]...之中
for (int i = 1; i < N; i++) {
for (int j = i; j > 0 && less(a[j], a[j-1]); j--) {
exch(a, j, j-1);
}
}
}
}
對於0到N-1之間的每一個i,將a[i]與a[0]到a[i-1]中比它小的所有元素依次有序地交換。在索引i由左向右變化的過程中,它左側的元素總是有序的,所以當i達到數組的右端時排序就完成了。

3.算法分析
命題:對於隨機排列的長度為N且主鍵不重復的數組,平均情況下插入排序需要~N2/4次比較以及~N2/4次交換。最壞情況下需要~N2/2次比較和~N2/2次交換,最好情況下需要N-1次比較和0次交換。
證明:通過一個NxN的軌跡表可以很容易就得到交換和比較的次數。最壞情況下對角線之下所有的元素都需要移動位置,最好情況下都不需要。對於隨機排列的數組,在平均情況下每個元素都可能向後移動半個數組的長度,因此交換總數是對角線之下的元素總數的二分之一。
比較的總次數是交換的次數加上一個額外的項,該項為N減去被插入的元素正好是已知的最小元素的次數。在最壞情況下(逆序數組),這一項相對於總數可以忽略不計;在最好情況下(數組已經有序),這一項等於N-1.
4.總結
我們要考慮的更一般的情況是部分有序的數組。倒置指的是數組中的兩個順序顛倒的元素。比如EXAMPLE中有11對倒置:E-A、X-A、X-M、X-P、X-L、X-E、M-L、M-E、P-L、P-E以及L-E。如果數組中倒置的數量小於數組大小的某個倍數,那麼我們說這個數組是部分有序的。下面是幾種典型的部分有序的數組:
•數組中每個元素距離它的最終位置都不遠;
•一個有序的大數組接一個小數組;
•數組中只有幾個元素的位置不正確。
插入排序對這樣的數組很有效,而選擇排序則不然。事實上,當倒置的數量很少時,插入排序很可能比本章中的其他任何算法都要快。總的來說,插入排序對於部分有序的數組十分高效,也很適合小規模數組。這很重要,因為這些類型的數組在實際應用中經常出現,而且它們也是高級排序算法的中間過程。
命題:插入排序需要的交換操作和數組中倒置的數量相同,需要的比較次數大於等於倒置的數量,小於等於倒置的數量加上數組的大小再減一。
證明:每次交換都改變了兩個順序顛倒的元素的位置,相當於減少了一對倒置,當倒置數量為0時,排序就完成了。每次交換都對應著一次比較,且1到N-1之間的每個i都可能需要一次額外的比較(在a[i]沒有達到數組的左端時)。
【源碼下載】
 Android開發文摘集合1,android文摘集合
Android開發文摘集合1,android文摘集合
Android開發文摘集合1,android文摘集合作者:張明雲 原標題:Android 開發中,有哪些坑需要注意? 作者github主頁:zmywly8866.gith
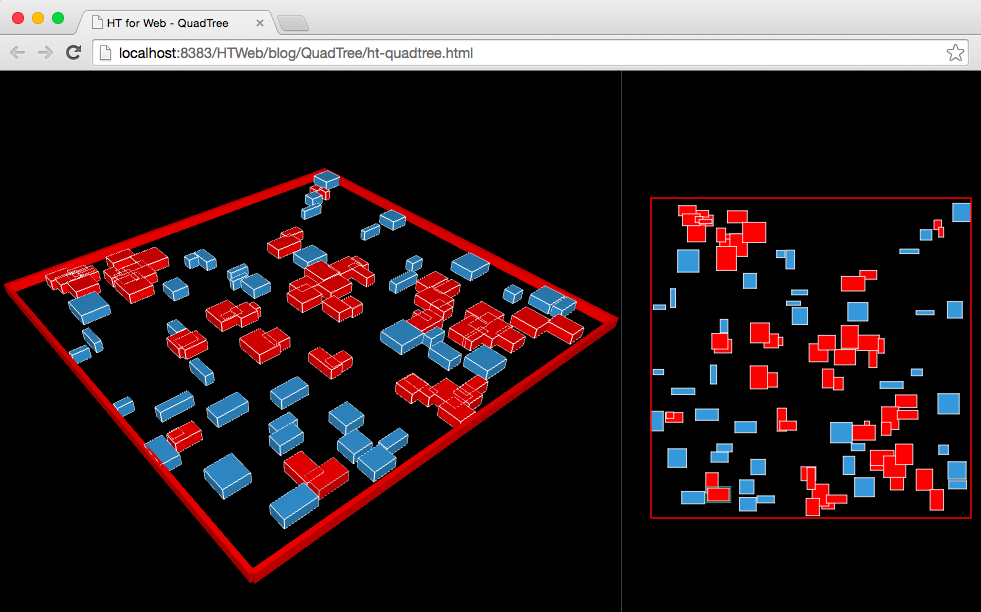 HTML5實現3D和2D可視化QuadTree四叉樹碰撞檢測
HTML5實現3D和2D可視化QuadTree四叉樹碰撞檢測
HTML5實現3D和2D可視化QuadTree四叉樹碰撞檢測QuadTree四叉樹顧名思義就是樹狀的數據結構,其每個節點有四個孩子節點,可將二維平面遞歸分割子區域。Qua
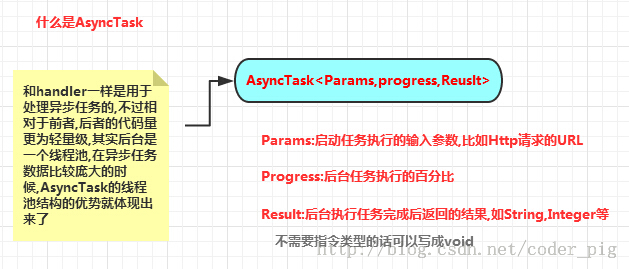 android AsynTask處理返回數據和AsynTask使用get,post請求,androidasyntask
android AsynTask處理返回數據和AsynTask使用get,post請求,androidasyntask
android AsynTask處理返回數據和AsynTask使用get,post請求,androidasyntaskAndroid是一個單線程模型,Android界面(
 A DB2 Performance Tuning Roadmap--Q-BASED A/A IMPLEMENATION
A DB2 Performance Tuning Roadmap--Q-BASED A/A IMPLEMENATION
A DB2 Performance Tuning Roadmap--Q-BASED A/A IMPLEMENATIONWhy Active/Active ? - Bus