編輯:關於android開發
1.基本思想
首先,找到數組中最小的那個元素,其次,將它和數組的第一個元素交換位置(如果第一個元素就是最小元素那麼它就和自己交換)。再次,在剩下的元素中找到最小的元素,將它與數組的第二個元素交換位置。如此往復,直到將整個數組排序。這種方法叫做選擇排序,因為它在不斷地選擇剩余元素之中的最小者。
2.具體算法
/**
* 選擇排序
* @author huazhou
*
*/
public class Selection extends Model{
//將a[]按升序排列
public void sort(Comparable[] a){
int N = a.length; //數組長度
//將a[i]和a[i+1...N]中最小的元素交換
for (int i = 0; i < N; i++) {
int min = i; //最小元素的索引
for (int j = i+1; j < N; j++) {
if(less(a[j], a[min])){
min = j;
}
}
exch(a, i, min);
}
}
}
//對元素進行比較,如果v比w小則返回true
protected boolean less(Comparable v, Comparable w){
return v.compareTo(w) < 0;
}
//將元素交換位置
protected void exch(Comparable[] a, int i, int j){
Comparable t = a[i];
a[i] = a[j];
a[j] = t;
}
3.算法分析
命題:對於長度為N的數組,選擇排序需要大約N2/2次比較和N次交換
證明:可以通過算法的排序軌跡來證明這一點。我們用一張NxN的表格來表示排序的軌跡(見下圖),其中每個非灰色字符都表示一次比較。表格中大約一半的元素不是灰色的——即對角線和其上部分的元素。對角線上的每個元素都對應著一次交換。通過查看代碼我們可以更精確地得到,0到N-1的任意i都會進行一次交換和N-1-i次比較,因此總共有N次交換以及(N-1)+(N-2)+...+2+1=N(N-1)/2~N2/2次比較。


4.總結
總的來說,選擇排序是一種很容易理解和實現的簡單排序算法,它有兩個很鮮明的特點。
運行時間和輸入無關。為了找出最小的元素而掃描一遍數組並不能為下一遍掃描提供什麼信息。這種性質在某些情況下是缺點,因為使用選擇排序的人可能會驚訝地發現,一個已經有序的數組或是主鍵全部相等的數組和一個元素隨機排列的數組所用的排序時間竟然一樣長!我們將會看到,其他算法會更善於利用輸入的初始狀態。
數據移動是最少的。每次交換都會改變兩個數組元素的值,因此選擇排序用了N次交換——交換次數和數組的大小是線性關系。我們將研究的其他任何算法都不具備這個特征(大部分的增長數量級都是線性對數或是平方級別)。
PS:
此次算法文章皆為原創,轉載請注明出處,內容皆出自Robert Sedgewick的《算法》第四版。
【源碼下載】,項目是用androidstudio開發的,原因是運行項目需要用到重定位輸入符<,eclipse和as直接運行都無法帶上此符號,只能在命令窗口運行,as的自帶命令窗口比較方便。運行方法,在as的命令窗口cd進入sort | build | classes | main,然後輸入java Example < D:\tiny.txt,此D:為tiny.txt的完整路徑。以下是我機器上的運行結果:

 Android簡單的ListViewDemo及每個控件的點擊事件,listview控件點擊事件
Android簡單的ListViewDemo及每個控件的點擊事件,listview控件點擊事件
Android簡單的ListViewDemo及每個控件的點擊事件,listview控件點擊事件 main.xml主頁面布局 <?xml version
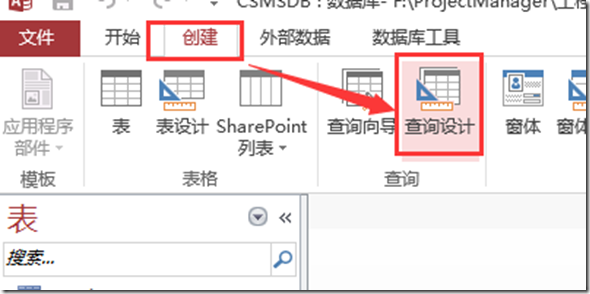 Access中使用sql查詢
Access中使用sql查詢
Access中使用sql查詢在ACCESS中使用SQL查詢語句檢查SQL語法時非常有用。 操作步驟如下: 【查詢設計】 直接關閉彈出的【顯示表】 找到【SQL視圖】:
 Android學習指南之三十二:Android主題(Theme)和風格(Style)
Android學習指南之三十二:Android主題(Theme)和風格(Style)
上一節講解的是Android中使用SAX和pull方式解析XML,本節的主要內容是Andr
 關於Ionic的安裝,Ionic安裝
關於Ionic的安裝,Ionic安裝
關於Ionic的安裝,Ionic安裝Ionic是一個前端的框架,幫助開發者使用HTML5, CSS3和JavaScript做出原生應用。 http://ionicfram