Android教程網 >> Android技術 >> Android開發 >> 關於android開發 >> Android 自定義View高級特效，神奇的貝塞爾曲線

Android 自定義View高級特效，神奇的貝塞爾曲線

編輯：關於android開發

Android 自定義View高級特效，神奇的貝塞爾曲線

效果圖

效果圖中我們實現了一個簡單的隨手指滑動的二階貝塞爾曲線，還有一個復雜點的，穿越所有已知點的貝塞爾曲線。學會使用貝塞爾曲線後可以實現例如QQ紅點滑動刪除啦，360動態球啦，bulabulabula~

什麼是貝塞爾曲線？

貝賽爾曲線（Bézier曲線）是電腦圖形學中相當重要的參數曲線。更高維度的廣泛化貝塞爾曲線就稱作貝塞爾曲面，其中貝塞爾三角是一種特殊的實例。貝塞爾曲線於1962年，由法國工程師皮埃爾·貝塞爾（Pierre Bézier）所廣泛發表，他運用貝塞爾曲線來為汽車的主體進行設計。貝塞爾曲線最初由Paul de Casteljau於1959年運用de Casteljau算法開發，以穩定數值的方法求出貝塞爾曲線。

讀完上述貝塞爾曲線簡介我還是一頭霧水，來個示例呗。

示例

線性貝塞爾曲線

給定點P0、P1，線性貝塞爾曲線只是一條兩點之間的直線。這條線由下式給出：

二次方貝塞爾曲線

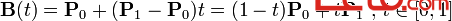
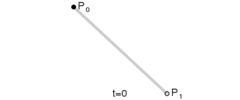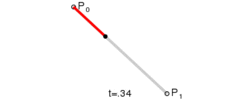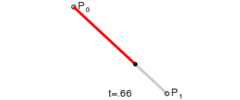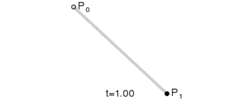
二次方貝塞爾曲線的路徑由給定點P0、P1、P2的函數B（t）追蹤：

三次方貝塞爾曲線

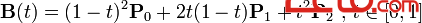
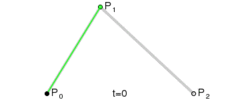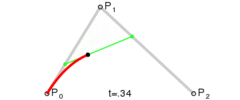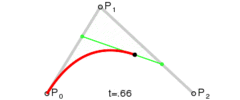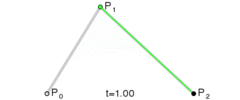
P0、P1、P2、P3四個點在平面或在三維空間中定義了三次方貝塞爾曲線。曲線起始於P0走向P1，並從P2的方向來到P3。一般不會經過P1或P2；公式如下：

N次方貝塞爾曲線

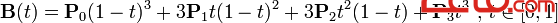
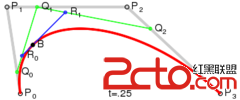
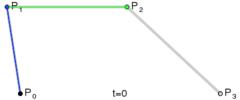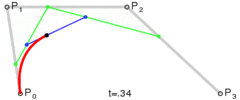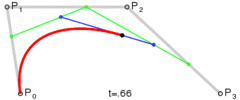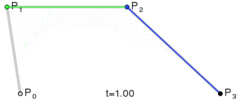
身為三維生物超出三維我很方，這裡只給示例圖。想具體了解的同學請左轉度娘。

就當沒看過上面

Android在API=1的時候就提供了貝塞爾曲線的畫法，只是隱藏在Path#quadTo()和Path#cubicTo()方法中，一個是二階貝塞爾曲線，一個是三階貝塞爾曲線。當然，如果你想自己寫個方法，依照上面貝塞爾的表達式也是可以的。不過一般沒有必要，因為Android已經在native層為我們封裝好了二階和三階的函數。

從一個二階貝塞爾開始

自定義一個BezierView

初始化各個參數，花3s掃一下即可。

    private Paint mPaint;
    private Path mPath;
    private Point startPoint;
    private Point endPoint;
    // 輔助點
    private Point assistPoint;
        public BezierView(Context context) {
        this(context, null);
    }

    public BezierView(Context context, AttributeSet attrs) {
        this(context, attrs, 0);
    }

    public BezierView(Context context, AttributeSet attrs, int defStyleAttr) {
        super(context, attrs, defStyleAttr);
        init(context);
    }

    private void init(Context context) {
        mPaint = new Paint();
        mPath = new Path();
        startPoint = new Point(300, 600);
        endPoint = new Point(900, 600);
        assistPoint = new Point(600, 900);
        // 抗鋸齒
        mPaint.setAntiAlias(true);
        // 防抖動
        mPaint.setDither(true);
    }

在onDraw中畫二階貝塞爾

        // 畫筆顏色
        mPaint.setColor(Color.BLACK);
        // 筆寬
        mPaint.setStrokeWidth(POINTWIDTH);
        // 空心
        mPaint.setStyle(Paint.Style.STROKE);
        // 重置路徑
        mPath.reset();
        // 起點
        mPath.moveTo(startPoint.x, startPoint.y);
        // 重要的就是這句
        mPath.quadTo(assistPoint.x, assistPoint.y, endPoint.x, endPoint.y);
        // 畫路徑
        canvas.drawPath(mPath, mPaint);
        // 畫輔助點
        canvas.drawPoint(assistPoint.x, assistPoint.y, mPaint);

上面注釋很清晰就不贅述了。示例中貝塞爾是可以跟著手指的滑動而變化，我一拍榴蓮，肯定是復寫了onTouchEvent()！

    @Override
    public boolean onTouchEvent(MotionEvent event) {
        switch (event.getAction()) {
            case MotionEvent.ACTION_DOWN:
            case MotionEvent.ACTION_MOVE:
                assistPoint.x = (int) event.getX();
                assistPoint.y = (int) event.getY();
                Log.i(TAG, "assistPoint.x = " + assistPoint.x);
                Log.i(TAG, "assistPoint.Y = " + assistPoint.y);
                invalidate();
                break;
        }
        return true;
    }

最後將我們自定義的BezierView添加到布局文件中。至此一個簡單的二階貝塞爾曲線就完成了。假設一下，在向下拉動的過程中，在曲線上增加一個“小超人”，360動態清理是不是就出來了呢？有興趣的可以自己拓展下。

以一個三階貝塞爾結束

天氣預報曲線圖示例

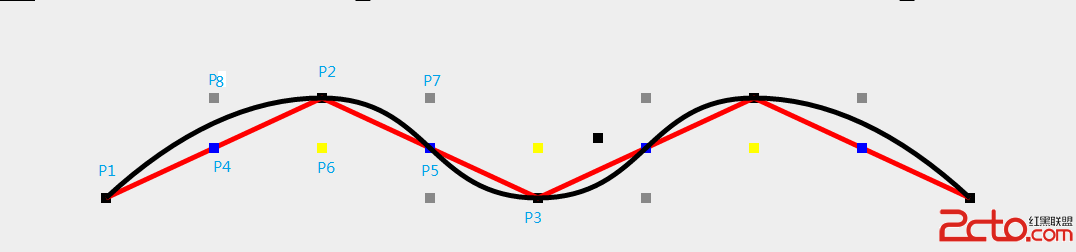
（圖一）
DEMO1
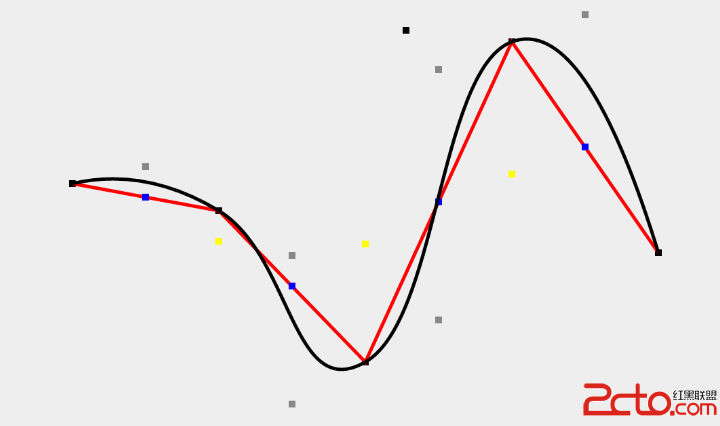
（圖二）
demo2

概述

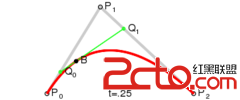
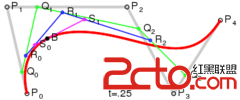
要想得到上圖的效果，需要二階貝塞爾和三階貝塞爾配合。具體表現為，第一段和最後一段曲線為二階貝塞爾，中間N段都為三階貝塞爾曲線。

思路

先根據相鄰點（P1，P2, P3）計算出相鄰點的中點(P4， P5)，然後再計算相鄰中點的中點(P6)。然後將（P4，P6, P5）組成的線段平移到經過P2的直線（P8，P2，P7）上。接著根據（P4，P6，P5，P2）的坐標計算出(P7，P8)的坐標。最後根據P7，P8等控制點畫出三階貝塞爾曲線。

點和線的解釋

黑色點：要經過的點，例如溫度藍色點：兩個黑色點構成線段的中點黃色點：兩個藍色點構成線段的中點灰色點：貝塞爾曲線的控制點紅色線：黑色點的折線圖黑色線：黑色點的貝塞爾曲線，也是我們最終想要的效果

聲明

為了方便講解以及讀者的理解。本篇以圖一效果為例進行講解。BezierView坐標都是根據屏幕動態生成的，想要圖二的效果只需修改初始坐標，不用對代碼做很大的修改即可實現。

那麼，開始吧！

初始化參數

    private static final String TAG = "BIZIER";
    private static final int LINEWIDTH = 5;
    private static final int POINTWIDTH = 10;

    private Context mContext;
    /** 即將要穿越的點集合 */
    private List mPoints = new ArrayList<>();
    /** 中點集合 */
    private List mMidPoints = new ArrayList<>();
    /** 中點的中點集合 */
    private List mMidMidPoints = new ArrayList<>();
    /** 移動後的點集合(控制點) */
    private List mControlPoints = new ArrayList<>();

    private int mScreenWidth;
    private int mScreenHeight;
    private void init(Context context) {
        mPaint = new Paint();
        mPath = new Path();
        // 抗鋸齒
        mPaint.setAntiAlias(true);
        // 防抖動
        mPaint.setDither(true);

        mContext = context;
        getScreenParams();
        initPoints();
        initMidPoints(this.mPoints);
        initMidMidPoints(this.mMidPoints);
        initControlPoints(this.mPoints, this.mMidPoints , this.mMidMidPoints);

    }

第一個函數獲取屏幕寬高就不說了。緊接著初始化了初始點、中點、中點的中點、控制點。我們一個個的跟進。首先是初始點。

    /** 添加即將要穿越的點 */
    private void initPoints() {
        int pointWidthSpace = mScreenWidth / 5;
        int pointHeightSpace = 100;
        for (int i = 0; i < 5; i++) {
            Point point;
            // 一高一低五個點
            if (i%2 != 0) {
                point = new Point((int) (pointWidthSpace*(i + 0.5)), mScreenHeight/2 - pointHeightSpace);
            } else {
                point = new Point((int) (pointWidthSpace*(i + 0.5)), mScreenHeight/2);
            }
            mPoints.add(point);
        }
    }

這裡循環創建了一高一低五個點，並添加到List mPoints中。上文說道圖一到圖二只需修改這裡的初始點即可。

    /** 初始化中點集合 */
    private void initMidPoints(List points) {
        for (int i = 0; i < points.size(); i++) {
            Point midPoint = null;
            if (i == points.size()-1){
                return;
            }else {
                midPoint = new Point((points.get(i).x + points.get(i + 1).x)/2, (points.get(i).y + points.get(i + 1).y)/2);
            }
            mMidPoints.add(midPoint);
        }
    }

    /** 初始化中點的中點集合 */
    private void initMidMidPoints(List midPoints){
        for (int i = 0; i < midPoints.size(); i++) {
            Point midMidPoint = null;
            if (i == midPoints.size()-1){
                return;
            }else {
                midMidPoint = new Point((midPoints.get(i).x + midPoints.get(i + 1).x)/2, (midPoints.get(i).y + midPoints.get(i + 1).y)/2);
            }
            mMidMidPoints.add(midMidPoint);
        }
    }

這裡算出中點集合以及中點的中點集合，小學數學題沒什麼好說的。唯一需要注意的是他們數量的差別。

    /** 初始化控制點集合 */
    private void initControlPoints(List points, List midPoints, List midMidPoints){
        for (int i = 0; i < points.size(); i ++){
            if (i ==0 || i == points.size()-1){
                continue;
            }else{
                Point before = new Point();
                Point after = new Point();
                before.x = points.get(i).x - midMidPoints.get(i - 1).x + midPoints.get(i - 1).x;
                before.y = points.get(i).y - midMidPoints.get(i - 1).y + midPoints.get(i - 1).y;
                after.x = points.get(i).x - midMidPoints.get(i - 1).x + midPoints.get(i).x;
                after.y = points.get(i).y - midMidPoints.get(i - 1).y + midPoints.get(i).y;
                mControlPoints.add(before);
                mControlPoints.add(after);
            }
        }
    }

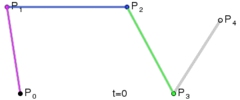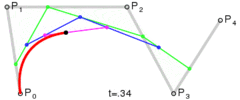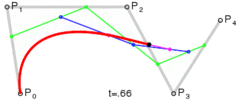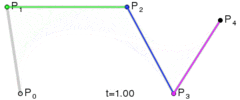
大家需要注意下這個方法的計算過程。以圖一（P2，P4, P6，P8）為例。現在P2、P4、P6的坐標是已知的。根據由於(P8, P2)線段由（P4， P6）線段平移而來，所以可得如下結論：P2 - P6 = P8 - P4 。即P8 = P2 - P6 + P4。其余同理。

畫輔助點以及對比折線圖

    @Override
    protected void onDraw(Canvas canvas) {
        super.onDraw(canvas);
        // ***********************************************************
        // ************* 貝塞爾進階--曲滑穿越已知點 **********************
        // ***********************************************************

        // 畫原始點
        drawPoints(canvas);
        // 畫穿越原始點的折線
        drawCrossPointsBrokenLine(canvas);
        // 畫中間點
        drawMidPoints(canvas);
        // 畫中間點的中間點
        drawMidMidPoints(canvas);
        // 畫控制點
        drawControlPoints(canvas);
        // 畫貝塞爾曲線
        drawBezier(canvas);

    }

可以看到，在畫貝塞爾曲線之前我們畫了一系列的輔助點，還有和貝塞爾曲線作對比的折線圖。效果如圖一。輔助點的坐標全都得到了，基本的畫畫就比較簡單了。有能力的可跳過下面這段，直接進入drawBezier(canvas)方法。基本的畫畫這裡只貼代碼，如有疑問可評論或者私信。

    /** 畫原始點 */
    private void drawPoints(Canvas canvas) {
        mPaint.setStrokeWidth(POINTWIDTH);
        for (int i = 0; i < mPoints.size(); i++) {
            canvas.drawPoint(mPoints.get(i).x, mPoints.get(i).y, mPaint);
        }
    }

    /** 畫穿越原始點的折線 */
    private void drawCrossPointsBrokenLine(Canvas canvas) {
        mPaint.setStrokeWidth(LINEWIDTH);
        mPaint.setColor(Color.RED);
        // 重置路徑
        mPath.reset();
        // 畫穿越原始點的折線
        mPath.moveTo(mPoints.get(0).x, mPoints.get(0).y);
        for (int i = 0; i < mPoints.size(); i++) {
            mPath.lineTo(mPoints.get(i).x, mPoints.get(i).y);
        }
        canvas.drawPath(mPath, mPaint);
    }

    /** 畫中間點 */
    private void drawMidPoints(Canvas canvas) {
        mPaint.setStrokeWidth(POINTWIDTH);
        mPaint.setColor(Color.BLUE);
        for (int i = 0; i < mMidPoints.size(); i++) {
            canvas.drawPoint(mMidPoints.get(i).x, mMidPoints.get(i).y, mPaint);
        }
    }

    /** 畫中間點的中間點 */
    private void drawMidMidPoints(Canvas canvas) {
        mPaint.setColor(Color.YELLOW);
        for (int i = 0; i < mMidMidPoints.size(); i++) {
            canvas.drawPoint(mMidMidPoints.get(i).x, mMidMidPoints.get(i).y, mPaint);
        }

    }

    /** 畫控制點 */
    private void drawControlPoints(Canvas canvas) {
        mPaint.setColor(Color.GRAY);
        // 畫控制點
        for (int i = 0; i < mControlPoints.size(); i++) {
            canvas.drawPoint(mControlPoints.get(i).x, mControlPoints.get(i).y, mPaint);
        }
    }

畫貝塞爾曲線

    /** 畫貝塞爾曲線 */
    private void drawBezier(Canvas canvas) {
        mPaint.setStrokeWidth(LINEWIDTH);
        mPaint.setColor(Color.BLACK);
        // 重置路徑
        mPath.reset();
        for (int i = 0; i < mPoints.size(); i++){
            if (i == 0){// 第一條為二階貝塞爾
                mPath.moveTo(mPoints.get(i).x, mPoints.get(i).y);// 起點
                mPath.quadTo(mControlPoints.get(i).x, mControlPoints.get(i).y,// 控制點
                        mPoints.get(i + 1).x,mPoints.get(i + 1).y);
            }else if(i < mPoints.size() - 2){// 三階貝塞爾
                mPath.cubicTo(mControlPoints.get(2*i-1).x,mControlPoints.get(2*i-1).y,// 控制點
                        mControlPoints.get(2*i).x,mControlPoints.get(2*i).y,// 控制點
                        mPoints.get(i+1).x,mPoints.get(i+1).y);// 終點
            }else if(i == mPoints.size() - 2){// 最後一條為二階貝塞爾
                mPath.moveTo(mPoints.get(i).x, mPoints.get(i).y);// 起點
                mPath.quadTo(mControlPoints.get(mControlPoints.size()-1).x,mControlPoints.get(mControlPoints.size()-1).y,
                        mPoints.get(i+1).x,mPoints.get(i+1).y);// 終點
            }
        }
        canvas.drawPath(mPath,mPaint);
    }

注釋太詳細，都沒什麼好寫的了。不過這裡需要注意判斷裡面的條件，對起點和終點的判斷一定要理解。要不然很可能會送你一個ArrayIndexOutOfBoundsException。

結束

貝塞爾曲線可以實現很多絢麗的效果，難的不是貝塞爾，而是good idea。

上一頁:Android 事件分發
下一頁:Android入門——Drawable與對應的資源xml的應用

關於android開發

開發入門初級開發中級開發高級開發關於android開發

相關文章