編輯:Android資訊
在 Android 開發中,矩陣是一個功能強大並且應用廣泛的神器,例如:用它來制作動畫效果、改變圖片大小、給圖片加各類濾鏡等。對於矩陣,Android 官方 SDK 為我們提供了一個強大的類 Matrix (還有 ColorMatrix )是一直困擾著我的問題,雖然大致能夠調用相應的 API ,但卻一直 get 不到其內在的梗。但是出來混總是別想著蒙混過關的,所以最近重新操起一年畢業的線性代數,再本著小事問老婆,大事問Google的心態,終於把多年不解的問題給破了。出於好記性不如爛筆頭的原因,便有了本文。
讀完本文,相信你能夠搞明白以下三個問題:
Matrix 是 Android SDK 提供的一個矩陣類,它代表一個 3 X 3 的矩陣(不懂矩陣為何物的童鞋就要自行 Google 了)。 Matrix 提供了讓我們獲得 Matrix 值的 API —— getValues

利用此 API 傳入一個長度為 9 的 float 數組,即可獲得矩陣中每個元素的值。那麼這 9 個浮點數的作用和意義是什麼呢,從 Android 官方文檔上看,它為這個數組中的每一個元素都定義了一個下標常量
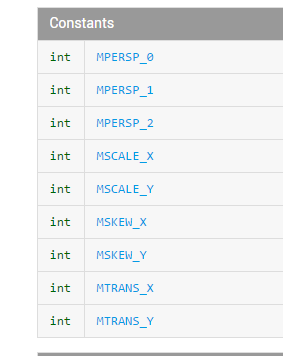
這個 9 個常量取值分別是 0 – 8
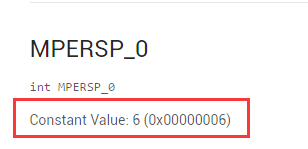
如果我們將這個 float 排成直觀的矩陣格式,那它將是下面這樣子的
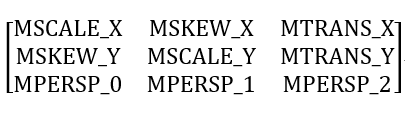
實際上我們平常利用 Matrix 來進行 Translate(平移)、Scale(縮放)、Rotate(旋轉)的操作,就是在操作著這個矩陣中元素的數值來達到我們想要的效果。但是現在問題來了,上面提到的平移、縮放、旋轉操作中,旋轉和縮放可以用乘法表示,而平移就只能用加法表示,而且 Matrix 是一個 3 X 3 的矩陣,實際上表示這些操作 2 X 2 的矩陣足矣!
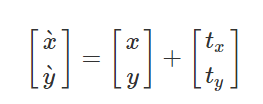
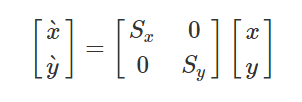
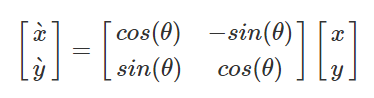
如上,可以依次看到平移、縮放、旋轉的矩陣,其中
至於上面矩陣的推導過程,網絡上很多,這裡就不去贅述了。以前到了這裡,我就會很納悶,為什麼 2 X 2 矩陣能干的事情,偏偏要用 3 X 3 矩陣去做,直到遇到前面提到的兩篇文章才有所領悟。
其實在計算機圖形應用涉及到幾何變換,主要包括平移、旋轉、縮放。以矩陣表達式來計算這些變換時,平移是矩陣相加,旋轉和縮放則是矩陣相乘。那些數學大神們為了方便計算,所以引入了一樣神器叫做齊次坐標(不懂的童鞋,老規矩自行搜索),將平移的加法合並用乘法表示。所以,2 X 2 的矩陣經過一番變換後,成了下面這樣的。



至此,我們可以得知為什麼 Matrix 是一個 3 X 3 的矩陣,其實 2 X 2 的矩陣是足以表示的,不過是為了方便計算而合並寫成了 3 X 3 的格式。
一個 Matrix 共有 9 個元素,那麼它每個元素的值發生改變會起到什麼作用呢?按照前面所示的齊次坐標轉換得到 3 X 3 的矩陣和 Android 文檔提供的官方結構相對應,我們不難看出下面的對應關系(其實從 Matrix 中每個位置的常量命名也可以看出來):



從這我們可以看出這個 Matrix 結構中的每個參數發揮著如下作用:
如果要進行代碼驗證的話,也非常簡單,例如直接只對 Matrix 做 Translate 的 API 調用操作,再將 Matrix 的信息打印到控制台,你會發現整個 Matrix 確實只有 MTRANS_X、MTRANS_Y 兩個位置的數字在發生變化。其他 Scale、Rotate、Skew 操作也是一樣,感興趣的童鞋可以自行代碼驗證一番。
至此,我們可以大致弄清矩陣每個元素的作用。至於 MPERSP_0、MPERSP_1、MPERSP_2 這三個參數,目前暫時不得而知,網上有文章說這三個參數控制著透視變換,但是文檔和 API 上都沒怎麼提及,所以還是有待驗證研究的,有明白的童鞋不妨留言賜教一下,不勝感激。
按照第一小節裡面通過齊次坐標轉換而來的矩陣方程可以知道,假設一根線執行了平移操作,相當於線上每個點的坐標被下方的矩陣左乘。(縮放和旋轉操作也是同理)
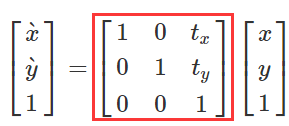
如果要進行同時縮放、平移之類的符合變化操作,也無非就是選取相應的矩陣做左乘操作。為了加深矩陣變換對應 Matrix API 調用的理解,直接通過下面的一個自定義的動畫效果和代碼來講解好了。
public class SimpleCustomAnimation extends Animation {
private int mWidth, mHeight;
@Override
public void initialize(int width, int height, int parentWidth, int parentHeight) {
super.initialize(width, height, parentWidth, parentHeight);
this.mWidth = width;
this.mHeight = height;
}
@Override
protected void applyTransformation(float interpolatedTime, Transformation t) {
Matrix matrix = t.getMatrix();
matrix.preScale(interpolatedTime, interpolatedTime);//縮放
matrix.preRotate(interpolatedTime * 360);//旋轉
//下面的Translate組合是為了將縮放和旋轉的基點移動到整個View的中心,不然系統默認是以View的左上角作為基點
matrix.preTranslate(-mWidth / 2, -mHeight / 2);
matrix.postTranslate(mWidth / 2, mHeight / 2);
}
}
熟悉動畫這塊的童鞋肯定知道,Animation 就是通過不斷改變 applyTransformation 函數傳入的 Matrix 來實現各種各樣的動畫效果的,通過上面 applyTransformation 寥寥的幾行 Matrix 的復合變換操作可以得到如下效果
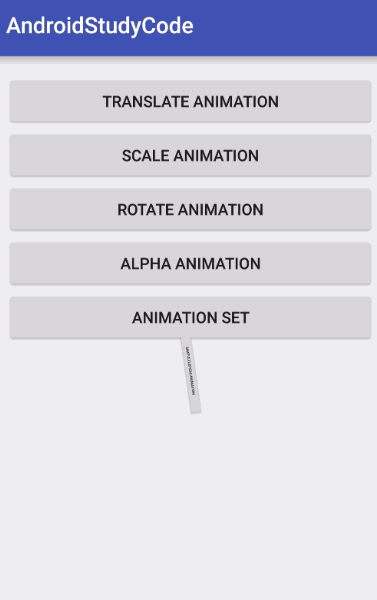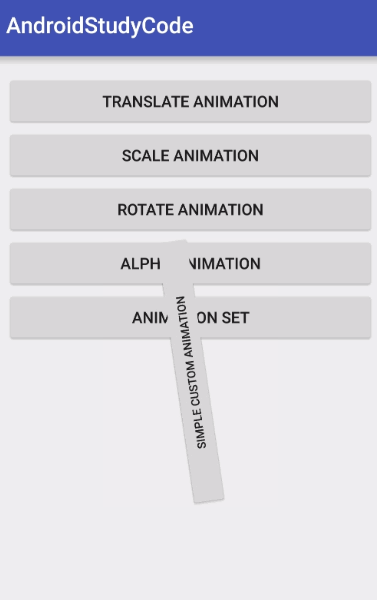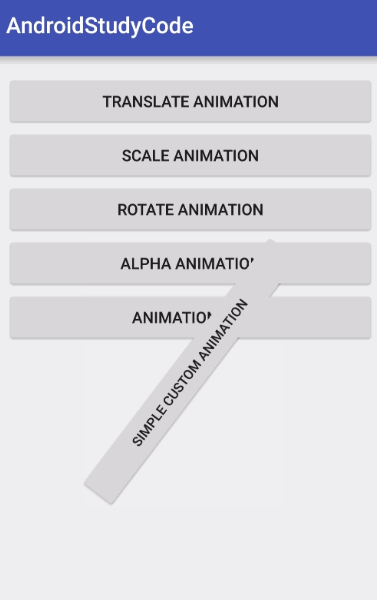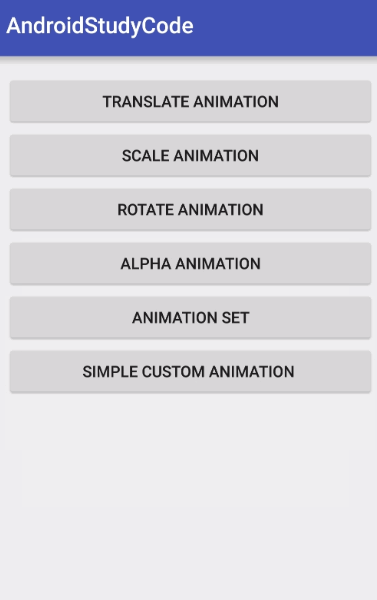
實際上這幾行代碼用矩陣來表示就相當於如下所示:
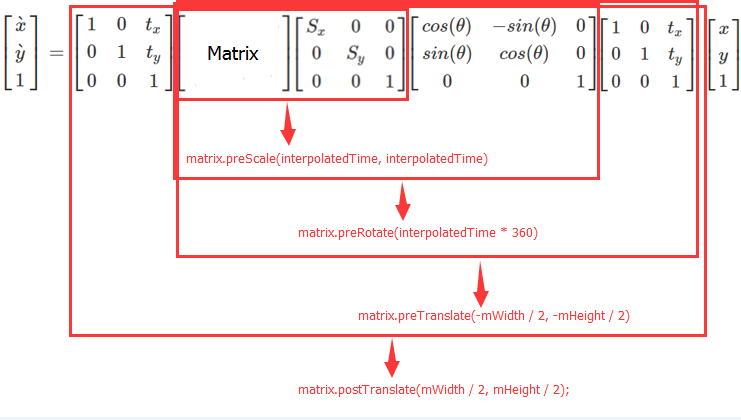
關於代碼的作用上邊已經給出了注釋,這裡就不多寫了。主要還是要弄明白 Matrix 復合變換中 pre 、 post 等操作與其對應的矩陣發生的左乘、右乘變化。
到此,整篇文章已經完結,相信已經能夠讓你明白開頭提到的三個問題。其實我們也可以發現,Google 封裝了 Matrix 已經是很完美了,幾乎屏蔽了所有的數學細節,使得我這種數學水平一般的開發者也能夠去調用相應的 API 實現一些簡單的效果。雖然被封裝得很完美,但掌握相應的一些原理,依舊可以幫你更好的理解一些技術實現,此次加深了對 Matrix 一些操作的理解,幫我自己解決了以前不少的困惑,不知道有沒有幫你 get 到一些什麼呢?
上面給的示例代碼很簡單,復制黏貼即可運行玩耍,實在需要直接運行源碼的童鞋就到 https://github.com/D-clock/AndroidStudyCode 找吧!
 Android include標簽方法淺析
Android include標簽方法淺析
本文將介紹在Android中如何使用include標簽來更便捷地重用布局代碼,從而減少冗余的Android代碼。 在一個Android項目中我們可能會需要用到相同
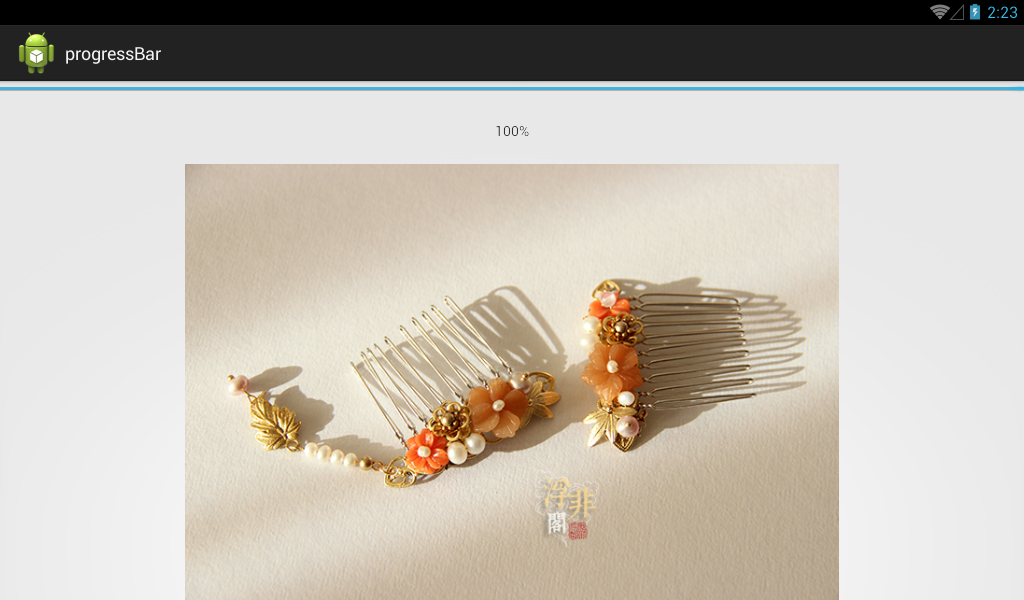 Android文件下載之進度檢測
Android文件下載之進度檢測
近期因為項目的需要,研究了一下Android文件下載進度顯示的功能實現,接下來就和大家一起分享學習一下,希望對廣大初學者有幫助。先上效果圖: 上方的藍色進度條,
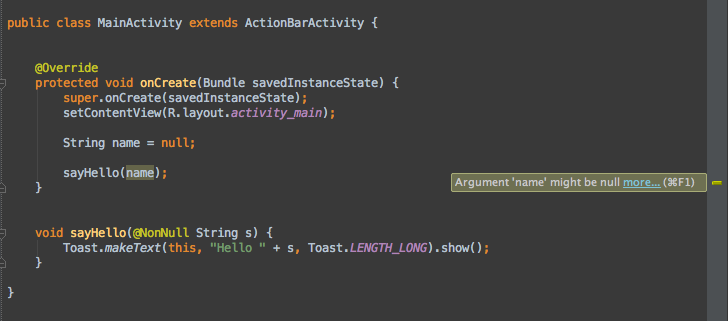 Android Support Annotations 使用詳解
Android Support Annotations 使用詳解
在Android Support Library19.1版本中,Android工具小組引入了幾個很酷的注解類型,供開發者在工程中使用。Support Librar
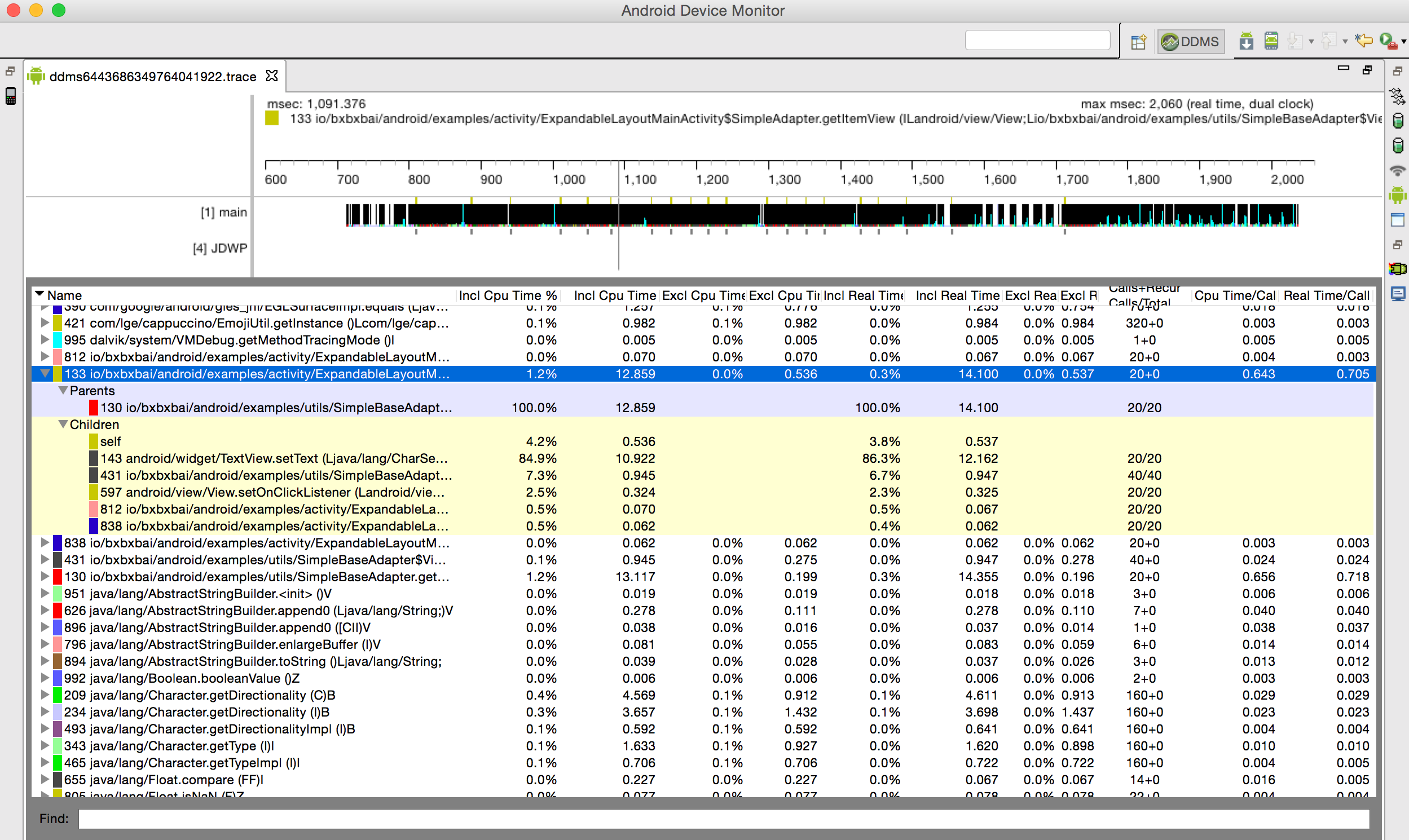 正確使用Android性能分析工具——TraceView
正確使用Android性能分析工具——TraceView
前面唠叨 最近公司app中有些列表在滑動的時候會有卡頓現象,我就開始著手解決這些問題,解決問題之前首先要分析列表滑動的性能瓶頸在什麼地方。因為之前不會正確使用Tr