編輯:關於Android編程
1. 引言
學術界普遍認為絕對不能選用e=3作為RSA公鑰指數,就好像說我們再也不能用md5一樣。但實際上,md5今天仍然廣泛使用。一個密碼算法在理論上被攻破,並不等於實踐中就一定會有安全風險。比如,md5作為一種密碼哈希函數,理論上它必須滿足三個性質:(1) 輸出的均勻分布性;(2) 抗碰撞攻擊;(3) 抗原像攻擊。當王小雲發現了md5不滿足性質(2)之後,理論上md5算法就被攻破——md5將從“密碼哈希函數”的家族中退出。盡管如此,我們的軟件系統中若使用了md5,就真的不安全了嗎?非也!因為實踐中的md5主要用於計算登錄密碼的摘要、數字簽名摘要,這些都只是依賴於md5的性質(3),只要仍然滿足抗原像攻擊,md5的實踐安全性就不會受到影響。
對於RSA算法,由於大多數軟件系統都可能基於openssl來開發,而openssl的低級版本一般會將e=3作為默認的RSA公鑰指數。選取小公鑰指數主要是為了提高加密或簽名驗證的性能,比如選e=3只需要2次模乘(ModMul),而隨機選擇的e(假設n是1024-bit)則大概需要1000次模乘。正因為如此,選用小公鑰指數的RSA在簽名驗證和加密操作上要比ECC算法(ANSI X9.62)高效得多。
那麼,選用e=3對PKCS#1的安全性有多大影響呢?在實現RSA算法時,只要不局限於自己對RSA的教科書式理解,比如遵循了PKCS#1 v2.1/v1.5 (2002/1993)或IEEE P1363的建議,或者使用公開的密碼算法庫(如OpenSSL),那麼你幾乎可以放心使用e=3。我所得結論是來自於我對RSA誕生以來學術界及業界針對小公鑰指數(e=3)的安全性分析。
2. e=3的安全性分析
(1) Hastad攻擊
Hastad描述的攻擊經常也被稱為廣播攻擊[1]。
攻擊場景:如果Alice打算將消息M加密發送給一組用戶,並且這組用戶選擇的公鑰指數e=3,那麼攻擊者Malice可以通過截獲3個密文
C1 = M^3 mod N1, C2 = M^3 mod N2, C3 = M^3 mod N3
便能夠有效地恢復出明文M。Hastad進一步指出,即使Alice在加密M之前對M進行了f運算(這裡f是一個公開的多項式函數),攻擊者仍然能有效地恢復出明文M。所以建議在進行消息填充時一定要選擇隨機化填充方法,比如OAEP[2],而不是一個確定的填充方法。
影響:PKCS#1 v2.1和v1.5均不受此攻擊的影響。
(2) Franklin-Reiter攻擊
Franklin-Reiter攻擊是一種明文相關性攻擊[3]。
攻擊場景:假設Bob的公鑰為(3, N),Alice發送消息M1和M2給Bob,並且M1 = f(M2) mod N,f是一個已知的多項式。那麼攻擊者Malice可以截獲密文
C1 = M1^3 mod N, C2 = M2^3 mod N
便能夠有效地恢復出明文M。所以建議明文在加密前一定要做隨機化處理。
影響:PKCS#1 v2.1和v1.5均不受此攻擊的影響。
(3) Coppersmith攻擊
首先我們介紹Coppersmith發現的短填充攻擊[4]。
攻擊場景:假設Bob的公鑰為(3, N),Alice發送消息M給Bob。消息M的填充方法是遵循PKCS#1 v1.5,即在消息尾部或頭部直接填充隨機串。如果攻擊者截獲到Alice發送給Bob的關於消息M的兩個不同的密文,即
C1 = (0002||r1||M)^3 mod N, C2 = (0002||r2||M)^3 mod N
如果填充的隨機串r的長度低於消息長度的1/9,那麼攻擊者便能夠有效地恢復出明文M。注意該攻擊對e = 65537無效。
影響:PKCS#1 v2.1不受影響,但PKCS#1 v1.5受此攻擊的影響。
[補充說明] Coppersmith在密碼分析領域做了很多傑出的工作,比如Coppersmith定理[4]已經成為一個密碼分析工作的奠基石。
Coppersmith定理:令N為大整數,f是度為e的多項式。給定N和f,可以有效地計算出方程f(x)=0 mod N所有小於N^(1/e)的解。
應用該定理,另一個簡單的攻擊如下:當e=3時,給定一個密文,如果攻擊者已知2/3的明文比特,則能恢復出整個明文。
(4) BDF攻擊
BDF攻擊[5]是針對私鑰d在部分暴露之後的攻擊。
攻擊結論:令(N, d)為私鑰,N的長度為n-bit。假若d的n/4個低位比特信息被洩露,那麼在e < sqrt(N)條件下,攻擊者可以有效地恢復出私鑰d。
另外值得一提的是,如果e = 3,我們很容易知道d的取值范圍,而且這個取值范圍的區間為sqrt(N)量級。這也就是說,如果e = 3,RSA就天然地洩露了d的一半比特位信息,只不過洩露的是高位比特,而不是低位比特。但是目前還沒有發現針對d的高位比特洩露的有效攻擊。
影響:PKCS#1 v2.1和v1.5均不受此攻擊的影響。
(5) 其它攻擊
關於RSA的其它相關攻擊,如小私鑰指數攻擊、共模攻擊、盲化攻擊、時間攻擊等,請參見[6, 7].
3. 結論
(I) 對於RSA加密來說,如果在實現上遵循PKCS#1 v2.1 (OAEP填充),目前還沒有發現有效的攻擊;但如果是遵循PKCS#1 v1.5 (明文尾部直接填充),那麼存在Coppersmith攻擊。
(II) 對於RSA簽名來說,目前對於PKCS#1 v2.1 (PSS填充)和PKCS#1 v1.5 (填充方法:0001FF...FF00||ASN.1||H(M)) 來說都還沒有發現有效的攻擊。
綜上所述,選用e=3作為RSA的公鑰指數,只要使用正確,目前仍然是安全的。
附1: 關於e=65537 (0x10001) 的說明
NIST SP800-78 Rev 1 (2007) 曾強調“不允許使用比65537更低的公鑰指數e”,但PKCS#1卻從未有過類似的建議。e=65537=(2^16+1),其簽名/加密運算只需要17次模乘,性能也算不錯。但我認為選這個值的目的只是一個介於小指數攻擊和運算效率之間的一個折中考慮,即以防萬一將來有一天"e=3"被攻破而僥幸"e=65537"可能還是安全的。
 Android自定義控件實現隨手指移動的小球
Android自定義控件實現隨手指移動的小球
一個關於自定義控件的小Demo,隨著手指移動的小球。先看下效果圖:實現代碼如下:1.自定義控件類package com.dc.customview.view;import
 Android入門教程之創建樣式與主題
Android入門教程之創建樣式與主題
一、前言作為一個安卓開發者,我們一般把焦點放在app的功能上。但是僅僅有功能是不夠的,界面和功能一樣重要。有兩種方法可以改變app的外觀。第一種就是直接在xml中直接修改
 Android入門:多線程斷點下載詳細介紹
Android入門:多線程斷點下載詳細介紹
本案例在於實現文件的多線程斷點下載,即文件在下載一部分中斷後,可繼續接著已有進度下載,並通過進度條顯示進度。也就是說在文件開始下載的同時,自動創建每個線程的下載進度的本地
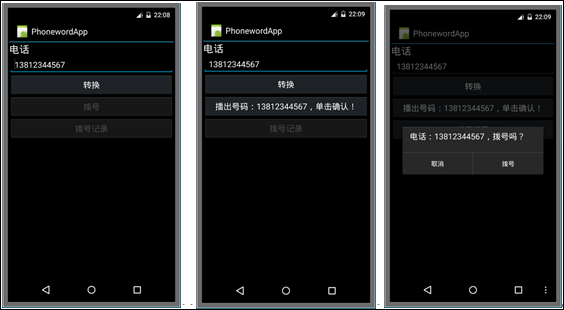 第1個Android應用程序 Android制作簡單單頁導航
第1個Android應用程序 Android制作簡單單頁導航
本例子演示如何添加一個簡單的單頁導航,在此基礎上,再演示如何在第2個頁面中顯示第1個頁面中撥打過的所有電話號碼。(1)通過該例子理解Android App的基本架構。(2