背景

之前在網上搜索了好多好多關於CNN，卷積神經網絡的文章，很多都講如何卷積、卷積層如何操作、具體如何進行卷積計算、卷積的好處。我也在此之前走了好多彎路，已經很了解如何卷積了，但是卻不知道物理意義上，卷積與神經網絡之間的聯系。

但是鑒於大量的文章在網絡上層出不窮地重復與累贅，更重要的是對於 卷積神經網絡 一詞當中，很多人都忽略了 神經網絡 而去強調如何 卷積，因此本文主要講述卷積神經網絡中最重要的部分， 神經網絡。希望看完這篇文章和相關卷積神經網絡ConvsNet的人能夠搞懂 NN 與 Conv 之間的聯系與物理意義。

1.人工神經網絡

1.1 神經元模型

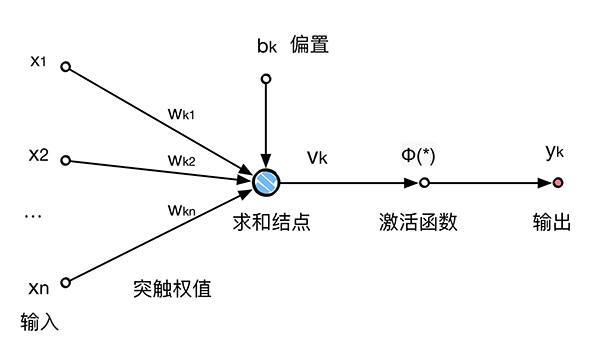
神經元是神經網絡操作的基本信息處理單位。下圖給出了神經元的模型model，這張圖是後續章節單重將要探討的設計（人工）神經網絡Big Family的基礎。我們在這裡給出了神經元模型的三種基本元素：

突觸 或者 鏈接鏈集， 每一個都由其 權值 或者 強度 作為特征。具體來說，在連接到神經元k的突觸 j 上的輸入信號 xj 被乘以 k 的突觸權值 wkj。 注意突觸權值 wkj 下標的寫法很重要。第一個下標指正在研究的這個神經元，第二個下標指權值所在的突觸的輸入端。和人腦的突觸不一樣的是，人工神經元的突觸權值只有一個范圍，可以取正值也可以取負值。

加法器，用於求輸入信號干杯神經元的相應突觸加權的和。這個操作構成一個線性組合器。

激活函數，用來限制神經元輸出振幅。由於通過激活函數將輸出信號壓制（限制）到允許范圍之內的一定值，故而激活函數也被稱之為壓制函數。通常，一個神經元輸出的正常幅度范圍可寫成單位區間 [0, 1] 或者另一種區間 [-1, +1]。

 

 

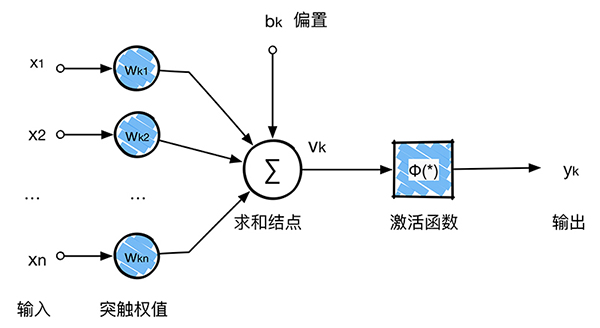
圖1的神經元也包括了一個外部偏置（bias），記為 bk。偏置 bk 的作用是根據其為正或為負，相應地增加或降低激活函數的網絡輸入。

用數學的公式來表示，我們可以用下面的方程描述上圖1的神經元 k：

uk=∑i=1mwkixi yk=ψ(uk+bk)

其中 x1,x2,...,xn 是輸入信號， wk1,wk2,...,wkn 是神經元k的突觸權值， uk 是輸入信號的線性組合器的輸出， bk為偏置，激活函數為 φ(?)， yk 是神經元輸出信號。偏置 bk 的作用是對模型中的線性組合器的輸出 uk 做仿射變換（affine transforrmation），如下所示：uk=uk+bk，其中 bk 一般為常數。

1.2 激活函數的類型

激活函數 φ(?)，通過誘導局部域 v 定義神經元輸出。根據本人的漏見與了解呵，在CNN當中主要用到的三種常見激活函數有（1）sigmoid function （2）tanh function （3） ReLU function:

1.sigmoid函數

此函數的圖形是S形狀的，在構造人工神經網絡中是最常見的激活函數，注意了，這裡在 卷積神經網絡 當中並不是最常見的，而是第三種 ReLu函數，因為ReLu計算起來更加簡單，可以大大縮小計算時間。回到sigmoid函數，它是嚴格遞增函數，在線性和非線性行為之間顯現出較好的平衡。sigmoid函數的第一個例子就是logistic函數，定義如下：

φ(v)=11+e?α?v

其中 α 是sigmoid函數的傾斜參數。修改參數 α 可以改變傾斜程度。在極限情況下，傾斜參數趨於無窮，sigmoid就變成了簡單的阈值函數。阈值函數僅取值0或1，而sigmoid的值域是0到1的連續區間。還要主要到sigmoid函數是可微分的。可微分性是神經網絡理論的一個重要的特征呵。

 

 

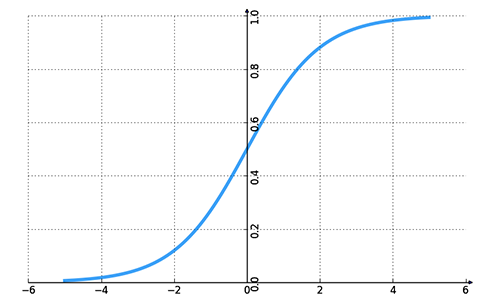
下面是更加科學的解釋為何激活函數使用sigmoid函數：

從數學意義來看，非線性的Sigmoid函數對中央區的信號增益較大，對兩側區的信號增益小，在信號的特征空間映射上，有很好的效果。

從神經科學上來看，中央區酷似神經元的興奮態，兩側區酷似神經元的抑制態，因而在神經網絡學習方面，可以將重點特征推向中央區，將非重點特征推向兩側區。

2.tanh函數，雙曲正切函數

tanh(x)=sinh(x)cosh(x)=ex?e?xex+e?x

雙曲函數出現於某些重要的線性微分方程的解中，譬如說定義懸鏈線和拉普拉斯方程。y=tanhx，定義域：R，值域：(?1,1)，奇函數，函數圖像為過原點並且穿越Ⅰ、Ⅲ象限的嚴格單調遞增曲線，其圖像被限制在兩水平漸近線y=1和y=?1之間。

與 sigmoid 不同的是，tanh 是0均值的。因此，實際應用中，tanh 會比 sigmoid 更好。

 

 

3.ReLU函數，ReLu(Rectified Linear Units)

ReLU(x)=max(0,x)

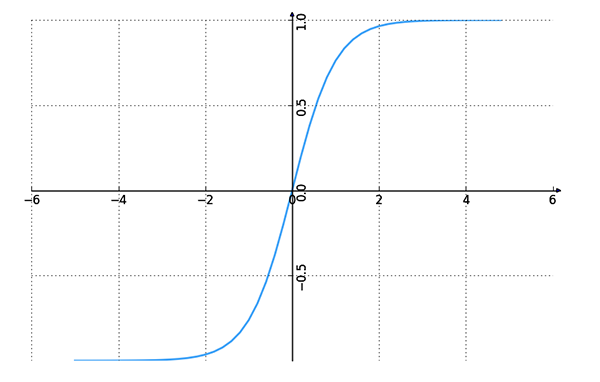
很顯然，從圖左可以看出，輸入信號<0時，輸出都是0，>0 的情況下，輸出等於輸入。w 是二維的情況下，使用ReLU之後的效果如下：

 

 

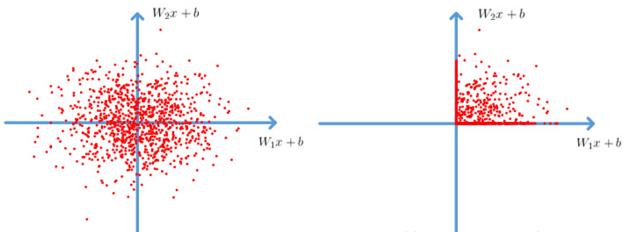
ReLU 的優點:

Krizhevsky et al. 發現使用 ReLU 得到的SGD的收斂速度會比 sigmoid/tanh 快很多。 相比於sigmoid/tanh，ReLU 只需要一個阈值就可以得到激活值，而不用去算一大堆復雜的運算。

ReLU 的缺點:

當在神經網絡中學習速率很大的時候，很有可能網絡中大部分神經元都會變成0。

當然，如果設置一個合適而且較小的學習速率的話，此類問題發生的情況也不會太頻繁。同時，為了解決這個問題，後面出現了各種ReLU的變種：Leaky-ReLU、P-ReLU、R-ReLU。

 

 

1.3 被看做有向圖的神經網絡

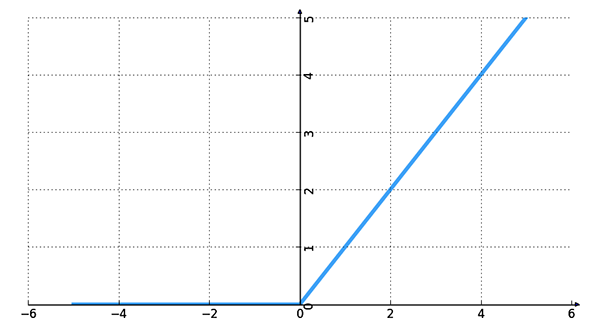
圖1中提供了構成人工神經元模型各個要素的功能描述。我們可以在補習生模型功能細節的條件下用信號流圖來簡化模型外觀。圖形中各部分的信號流動遵從三條基本規則。

信號僅僅沿定義好的箭頭方向在鏈接上流動。 節點信號等於經有連接進入的有關節點的所有信號的代數和。 節點信號沿著每個外向鏈接外向傳遞，此時傳遞的信號完全獨立於外向鏈接的傳遞函數。

 

 

1.4 反饋

 

 

上圖是一個單環反饋系統的信號流圖，在這裡只做簡單的介紹帶過。因為對CNN並沒有太大的關系，只是一個概念地存在著。輸入信號為xj(n)，內部信號為x′j(n)，輸出信號為yk(n)，他們都是離散時間變量n的函數。這個系統被假定位線性的，由算子A表示的向前通道和算子B表示的反饋通道組成。向前通道的輸出通過反饋通道來部分地影響自己的輸出。由上圖很容易得到這樣的輸入輸出關系：

yk(n)=A[x′j(n)] x′j(n)=yk(n)+B[xj(n)]

從上面兩個式子可以消去x_{j}^{‘}(n):

yk(n)=A1?AB[xj(n)]

OK。公式推導到這裡為止啦，反饋網絡現在用的最多的是在工控領域、模式識別中。

1.5 多層前饋網絡

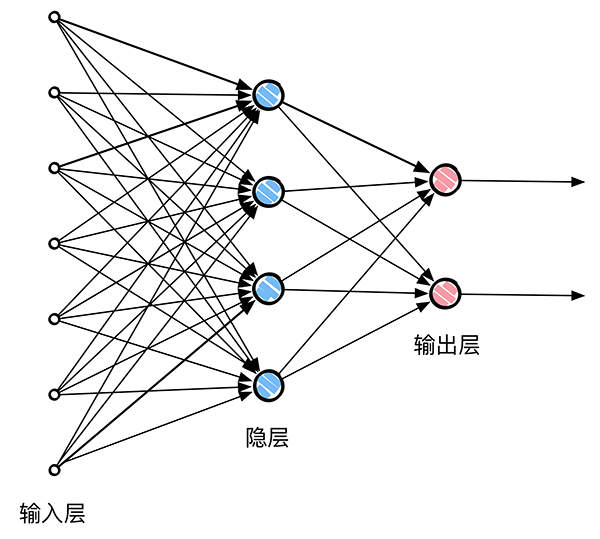
在分層網絡中，神經元以層的形式組織。相應的計算節點稱為隱藏神經元或隱藏單元。隱藏是指神經網絡的這一部分無論從網絡的輸入端或者輸出端都不能直接看到。隱藏神經元的功能是以某種有用的方式接入外部輸入和網絡輸出中的。

多層網絡可以根據其輸入引出高階統計特性， 即使網絡為局部連接，由於格外的突觸連接和額外的神經交互作用，也可以使網絡在不十分嚴格的意義下獲得一個全局關系。這也就是CNN使用局部連接之後還獲得很好的效果的原因。

 

 

在物理意義上，CNN其實也是上圖這樣的一個神經網絡，其卷積核就是權值的集合，例如一個卷積核是3*3大小，實際上是由9個權值組合而成的。通過大量的輸入進行訓練，為的就是得到這些權值，然後下一次有新的輸入的時候，直接由之前已經訓練好的權值和偏置對輸入進行計算，直接得到輸出。更加詳細的會在後續的面包中講解。

小結

到這裡為止，很重要的一點是認識到單一個神經元的模型定義，從輸入到求和，加上偏置值對求和進行微調，輸出前經過一個激活函數。現在我們已經很詳細地講解了一下激活函數φ(?)。那麼在這個模型當中，我們已經確定了激活函數φ(?)，輸入x1,x2,...,xn是確定的，未知量就剩下神經元k的突觸權值wk1,wk2,...,wkn ，bk 偏置。反向傳播算法（back propagation）就是為了求整個神經網絡當中的兩種未知變量：權值 w 和偏置 b。