編輯:關於Android編程
BinaryTree線索化二叉樹>
二叉樹是一種非線性結構,在之前實現的二叉樹遍歷中不管是遞歸還是非遞歸用二叉樹作為存儲結構時只能取到該結點的左孩子和右孩子,不能得到該結點的前驅和後繼。為了保存這種在遍歷中需要的信息,同時也為了充分利用結點中的空指針域,我們利用二叉樹中指向左右子樹的空指針來存放結點的前驅和後繼.同時在有n個結點的二叉鏈表中必定存在n+1個空鏈域.
那仫問題來了如何充分的利用這些空鏈域來實現線索化呢?
假設做如下規定:若結點有左子樹則其左孩子域指向該結點的左孩子,否則另左孩子指向其前驅;若結點有右子樹則其右孩子域指向該結點的右孩子,否則另右孩子域指向其後繼.為了實現這種構想我們需要增加兩個標志域_leftTag,_rightTag.

一.線索化及中序遍歷一棵樹
要線索化一顆二叉樹,最重要的就是在訪問了當前結點並確定當前結點的左孩子域或者右孩子域為空後如何找到當前結點的前一個結點也就是它的前驅,和當前結點的後繼.在這裡我們用到了一個_prev指針用來保存你訪問結點的前一個結點--如果當前結點的左子樹域為空則使當前結點的左孩子域指向_prev所指向的結點也就是當前結點的前驅;我們知道中序是按照左-根-右的順序遍歷的,如果當前結點的左訪問過了,根也訪問過了按照中序遍歷的順序接下來就應該訪問右了-_prev指針指向的是當前結點的前一個結點要訪問右則只需判斷_prev的右孩子域是否為空就可以了,如果為空則使_prev的右孩子域指向它的後繼.
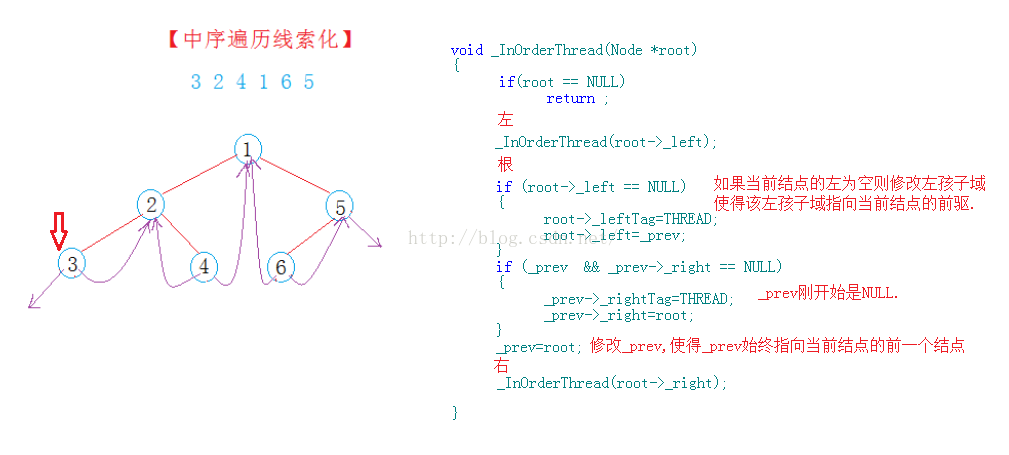
void _InOrderThread(Node *root)
{
if(root == NULL)
return ;
//左子樹
_InOrderThread(root->_left);
//根
if (root->_left == NULL)
{
root->_leftTag=THREAD;
root->_left=_prev;
}
if (_prev && _prev->_right == NULL)
{
_prev->_rightTag=THREAD;
_prev->_right=root;
}
_prev=root;
//右子樹
_InOrderThread(root->_right);
}
中序線索化一顆二叉樹後如何遍歷呢?和之前非遞歸的方法類似,使得cur指針指向該樹的左路結點,如果該結點有右子樹則訪問右子樹,如果沒有右子樹則繼續修改cur的值,使其指向當前結點的後繼.
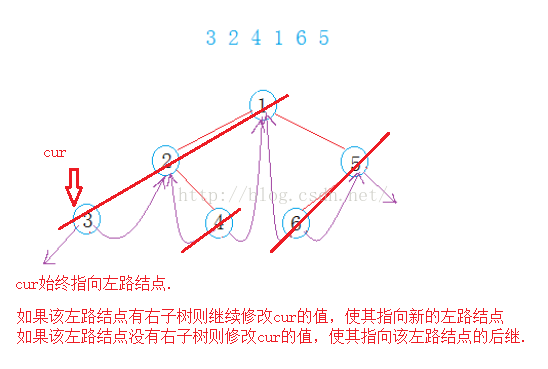
void _InOrder(Node *root)
{
if(root == NULL)
return ;
Node *cur=root;
while (cur)
{
//一路向左找到最左的結點.
while (cur->_leftTag == LINK)
{
cur=cur->_left;
}
cout<_data<<" ";
//有後繼
while (cur && cur->_rightTag == THREAD)
{
cur=cur->_right;
cout<_data<<" ";
}
//沒有後繼有右子樹
cur=cur->_right;
}
}
二.線索化及前序遍歷一棵樹>
前序遍歷的線索化類似中序遍歷的線索化,但是因為前序的順序是根-左-右,會因為遞歸太深導致棧溢出的問題,所以在遞歸線索化左子樹和右子樹的時候需要判斷當前結點的左右標志是否為LINK類型-是才遞歸線索化左子樹和右子樹.
void _PrevOrderThread(Node *root)
{
if(root == NULL)
return ;
if (root->_left == NULL)
{
root->_leftTag=THREAD;
root->_left=_prev;
}
if (_prev && _prev->_right == NULL)
{
_prev->_rightTag=THREAD;
_prev->_right=root;
}
_prev=root;
if(root->_leftTag == LINK) //防止棧溢出
_PrevOrderThread(root->_left);
if(root->_rightTag == LINK)
_PrevOrderThread(root->_right);
}
void _PrevOrder(Node *root)
{
if(root == NULL)
return ;
Node *cur=root;
while (cur)
{
while (cur && cur->_leftTag == LINK)
{
cout<_data<<" ";
cur=cur->_left;
}
cout<_data<<" ";
//將該樹的後繼當成子樹來訪問
cur=cur->_right;
//while (cur && cur->_rightTag == THREAD)
//{
// cur=cur->_right;
// cout<_data<<" ";
//}
//cur=cur->_right;
}
}
三.線索化及後序遍歷一棵樹>
在後序線索樹中找一個結點的前驅很容易直接用_prev就可以找到,那仫如何找一個結點的後繼呢?這時就比較棘手了
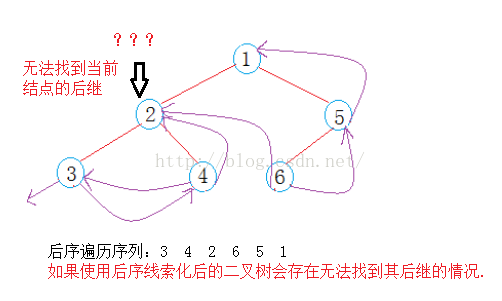
也就是說,在後序線索化樹上找後繼時需要知道結點雙親,此時我們可以使用三叉鏈表做存儲結構找到其雙親結點,其實還有一種思路就是逆向思維的方式----我們知道在後序遍歷線索二叉樹時有的時候是不容易找到一個結點的後繼的,如果我們按照根-右-左的順序逆序遍歷一顆線索二叉樹就會變的非常簡單了.
在實現中我只實現第二種思路即倒著訪問一顆後序線索化的二叉樹.
程序源代碼>
BinaryTreeThd.h
#pragma once
enum PointerTag
{
THREAD, //0:線索
LINK //1:指針
};
template
struct BinaryTreeThdNode
{
BinaryTreeThdNode(const T& x=T())
:_data(x)
,_left(NULL)
,_right(NULL)
,_leftTag(LINK)
,_rightTag(LINK)
{}
T _data;
BinaryTreeThdNode *_left;
BinaryTreeThdNode *_right;
PointerTag _leftTag; //左孩子線索化標志
PointerTag _rightTag; //右孩子線索化標志
};
template
class BinaryTreeThd
{
typedef BinaryTreeThdNode Node;
public:
BinaryTreeThd(const T *a,size_t size,const T& invalid)
:_root(NULL)
,_prev(NULL)
{
size_t index=0;
_root=_CreatTreeThd(a,size,index,invalid);
}
public:
void PrevOrderThread() //前序線索化二叉樹
{
_PrevOrderThread(_root);
}
void PrevOrder() //前序遍歷二叉樹
{
_PrevOrder(_root);
cout<_left=_CreatTreeThd(a,size,++index,invalid);
root->_right=_CreatTreeThd(a,size,++index,invalid);
}
return root;
}
protected:
void _PrevOrderThread(Node *root)
{
if(root == NULL)
return ;
if (root->_left == NULL)
{
root->_leftTag=THREAD;
root->_left=_prev;
}
if (_prev && _prev->_right == NULL)
{
_prev->_rightTag=THREAD;
_prev->_right=root;
}
_prev=root;
if(root->_leftTag == LINK) //防止棧溢出
_PrevOrderThread(root->_left);
if(root->_rightTag == LINK)
_PrevOrderThread(root->_right);
}
void _InOrderThread(Node *root)
{
if(root == NULL)
return ;
//左子樹
_InOrderThread(root->_left);
//根
if (root->_left == NULL)
{
root->_leftTag=THREAD;
root->_left=_prev;
}
if (_prev && _prev->_right == NULL)
{
_prev->_rightTag=THREAD;
_prev->_right=root;
}
_prev=root;
//右子樹
_InOrderThread(root->_right);
}
void _PostOrderThread(Node *root)
{
if(root == NULL)
return ;
_PostOrderThread(root->_left);
_PostOrderThread(root->_right);
if (root->_left == NULL)
{
root->_leftTag=THREAD;
root->_left=_prev;
}
if (_prev && _prev->_right == NULL)
{
_prev->_rightTag=THREAD;
_prev->_right=root;
}
_prev=root;
}
void _PrevOrder(Node *root)
{
if(root == NULL)
return ;
Node *cur=root;
while (cur)
{
while (cur && cur->_leftTag == LINK)
{
cout<_data<<" ";
cur=cur->_left;
}
cout<_data<<" ";
//將該樹的後繼當成子樹來訪問
cur=cur->_right;
//while (cur && cur->_rightTag == THREAD)
//{
// cur=cur->_right;
// cout<_data<<" ";
//}
//cur=cur->_right;
}
}
void _InOrder(Node *root)
{
if(root == NULL)
return ;
Node *cur=root;
while (cur)
{
//一路向左找到最左的結點.
while (cur && cur->_leftTag == LINK)
{
cur=cur->_left;
}
cout<_data<<" ";
//有後繼
while (cur && cur->_rightTag == THREAD)
{
cur=cur->_right;
cout<_data<<" ";
}
//沒有後繼有右子樹
cur=cur->_right;
}
}
//倒著遍歷後序線索化二叉樹
//根-右-左
void _PostOrder(Node *root)
{
if(root == NULL)
return ;
Node *cur=root;
while (cur)
{
while (cur && cur->_rightTag == LINK)
{
cout<_data<<" ";
cur=cur->_right;
}
cout<_data<<" ";
//有前驅
while (cur->_left && cur->_leftTag == THREAD)
{
cur=cur->_left;
cout<_data<<" ";
}
//有左子樹
cur=cur->_left;
}
}
protected:
Node *_root;
Node *_prev; //保存當前結點的前一個結點
};
test.cpp
void testBinaryTreeThd()
{
int array[15] = {1,2,'#',3,'#','#',4,5,'#',6,'#',7,'#','#',8};
size_t size=sizeof(array)/sizeof(array[0]);
BinaryTreeThd bt1(array,size,'#');
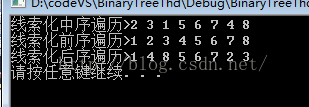
cout<<"線索化中序遍歷>";
bt1.InOrderThread();
bt1.InOrder(); //3 2 1 5 6 7 4 8
BinaryTreeThd bt2(array,size,'#');
cout<<"線索化前序遍歷>";
bt2.PrevOrderThread();
bt2.PrevOrder(); //1 2 3 4 5 6 7 8
BinaryTreeThd bt3(array,size,'#');
cout<<"線索化後序遍歷>";
bt3.PostOrderThread();
bt3.PostOrder(); //1 4 8 5 6 7 2 3
}
 android百度定位後顯示在地圖上點擊彈出氣泡
android百度定位後顯示在地圖上點擊彈出氣泡
1.到百度地圖頁面申請key,注意key和項目包名和數字簽名一一對應的。http://developer.baidu.com/map/index.php?title=%E
 微信運動 微信運動怎麼用
微信運動 微信運動怎麼用
微信運動是微信開發的基於第三方個人運動數據實現微信好友運動數據記錄和PK的一項服務,微信運動通過讀取第三方運動數據實現與微信好友運動數據PK,目前微信運動支
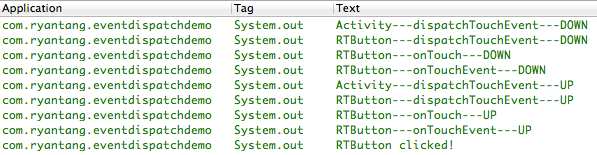 Android事件傳遞機制
Android事件傳遞機制
實驗環境OS X 10.9Eclipse(ADT)Android源碼版本:API Level 19(Android 4.4)Android事件構成在Android中,事件
 Android實現自定義輪播圖片控件示例
Android實現自定義輪播圖片控件示例
要完成一個輪播圖片,首先想到的應該是使用ViewPager來實現。ViewPager已經有了滑動的功能,我們只要讓它自己滾動。再加上下方的小圓點就行了。所以我們本次的自定