安卓自定義View進階-Matrix詳解

這應該是目前最詳細的一篇講解Matrix的中文文章了，在上一篇文章Matrix原理中，我們對Matrix做了一個簡單的了解，偏向理論，在本文中則會詳細的講解Matrix的具體用法，以及與Matrix相關的一些實用技巧。

Matrix方法表

按照慣例，先放方法表做概覽。

方法類別 相關API 摘要 基本方法 equals hashCode toString toShortString 比較、 獲取哈希值、 轉換為字符串 數值操作 set reset setValues getValues 設置、 重置、 設置數值、 獲取數值 數值計算 mapPoints mapRadius mapRect mapVectors 計算變換後的數值 設置(set) setConcat setRotate setScale setSkew setTranslate 設置變換 前乘(pre) preConcat preRotate preScale preSkew preTranslate 前乘變換 後乘(post) postConcat postRotate postScale postSkew postTranslate 後乘變換 特殊方法 setPolyToPoly setRectToRect rectStaysRect setSinCos 一些特殊操作 矩陣相關 invert isAffine(API21) isIdentity 求逆矩陣、 是否為仿射矩陣、 是否為單位矩陣 …

Matrix方法詳解

構造方法

構造方法沒有在上面表格中列出。

無參構造

Matrix ()

創建一個全新的Matrix，使用格式如下：

Matrix matrix = new Matrix();

通過這種方式創建出來的並不是一個數值全部為空的矩陣，而是一個單位矩陣,如下:

有參構造

Matrix (Matrix src)

這種方法則需要一個已經存在的矩陣作為參數，使用格式如下:

Matrix matrix = new Matrix(src);

創建一個Matrix，並對src深拷貝(理解為新的matrix和src是兩個對象，但內部數值相同即可)。

基本方法

基本方法內容比較簡單，在此處簡要介紹一下。

1.equals

比較兩個Matrix的數值是否相同。

2.hashCode

獲取Matrix的哈希值。

3.toString

將Matrix轉換為字符串: Matrix{[1.0, 0.0, 0.0][0.0, 1.0, 0.0][0.0, 0.0, 1.0]}

4.toShortString

將Matrix轉換為短字符串: [1.0, 0.0, 0.0][0.0, 1.0, 0.0][0.0, 0.0, 1.0]

數值操作

數值操作這一組方法可以幫助我們直接控制Matrix裡面的數值。

1.set

void set (Matrix src)

沒有返回值，有一個參數，作用是將參數Matrix的數值復制到當前Matrix中。如果參數為空，則重置當前Matrix，相當於reset()。

2.reset

void reset ()

重置當前Matrix(將當前Matrix重置為單位矩陣)。

3.setValues

void setValues (float[] values)

setValues的參數是浮點型的一維數組，長度需要大於9，拷貝數組中的前9位數值賦值給當前Matrix。

4.getValues

void getValues (float[] values)

很顯然，getValues和setValues是一對方法，參數也是浮點型的一維數組，長度需要大於9，將Matrix中的數值拷貝進參數的前9位中。

數值計算

1.mapPoints

void mapPoints (float[] pts)

void mapPoints (float[] dst, float[] src)

void mapPoints (float[] dst, int dstIndex,float[] src, int srcIndex, int pointCount)

計算一組點基於當前Matrix變換後的位置，(由於是計算點，所以參數中的float數組長度一般都是偶數的,若為奇數，則最後一個數值不參與計算)。

它有三個重載方法:

(1) void mapPoints (float[] pts) 方法僅有一個參數，pts數組作為參數傳遞原始數值，計算結果仍存放在pts中。

示例:

// 初始數據為三個點 (0, 0) (80, 100) (400, 300) 
float[] pts = new float[]{0, 0, 80, 100, 400, 300};

// 構造一個matrix，x坐標縮放0.5
Matrix matrix = new Matrix();
matrix.setScale(0.5f, 1f);

// 輸出pts計算之前數據
Log.i(TAG, "before: "+ Arrays.toString(pts));

// 調用map方法計算
matrix.mapPoints(pts);

// 輸出pts計算之後數據
Log.i(TAG, "after : "+ Arrays.toString(pts));

結果:

before: [0.0, 0.0, 80.0, 100.0, 400.0, 300.0]
after : [0.0, 0.0, 40.0, 100.0, 200.0, 300.0]

(2) void mapPoints (float[] dst, float[] src) ，src作為參數傳遞原始數值，計算結果存放在dst中，src不變。

如果原始數據需要保留則一般使用這種方法。

示例:

// 初始數據為三個點 (0, 0) (80, 100) (400, 300)
float[] src = new float[]{0, 0, 80, 100, 400, 300};
float[] dst = new float[6];

// 構造一個matrix，x坐標縮放0.5
Matrix matrix = new Matrix();
matrix.setScale(0.5f, 1f);

// 輸出計算之前數據
Log.i(TAG, "before: src="+ Arrays.toString(src));
Log.i(TAG, "before: dst="+ Arrays.toString(dst));

// 調用map方法計算
matrix.mapPoints(dst,src);

// 輸出計算之後數據
Log.i(TAG, "after : src="+ Arrays.toString(src));
Log.i(TAG, "after : dst="+ Arrays.toString(dst));

結果:

before: src=[0.0, 0.0, 80.0, 100.0, 400.0, 300.0]
before: dst=[0.0, 0.0, 0.0, 0.0, 0.0, 0.0]
after : src=[0.0, 0.0, 80.0, 100.0, 400.0, 300.0]
after : dst=[0.0, 0.0, 40.0, 100.0, 200.0, 300.0]

(3) void mapPoints (float[] dst, int dstIndex,float[] src, int srcIndex, int pointCount) 可以指定只計算一部分數值。

參數 摘要 dst 目標數據 dstIndex 目標數據存儲位置起始下標 src 源數據 srcIndex 源數據存儲位置起始下標 pointCount 計算的點個數

示例:

>

將第二、三個點計算後存儲進dst最開始位置。

// 初始數據為三個點 (0, 0) (80, 100) (400, 300)
float[] src = new float[]{0, 0, 80, 100, 400, 300};
float[] dst = new float[6];

// 構造一個matrix，x坐標縮放0.5
Matrix matrix = new Matrix();
matrix.setScale(0.5f, 1f);

// 輸出計算之前數據
Log.i(TAG, "before: src="+ Arrays.toString(src));
Log.i(TAG, "before: dst="+ Arrays.toString(dst));

// 調用map方法計算(最後一個2表示兩個點，即四個數值,並非兩個數值)
matrix.mapPoints(dst, 0, src, 2, 2);

// 輸出計算之後數據
Log.i(TAG, "after : src="+ Arrays.toString(src));
Log.i(TAG, "after : dst="+ Arrays.toString(dst));

結果:

before: src=[0.0, 0.0, 80.0, 100.0, 400.0, 300.0]
before: dst=[0.0, 0.0, 0.0, 0.0, 0.0, 0.0]
after : src=[0.0, 0.0, 80.0, 100.0, 400.0, 300.0]
after : dst=[40.0, 100.0, 200.0, 300.0, 0.0, 0.0]

2.mapRadius

float mapRadius (float radius)

測量半徑，由於圓可能會因為畫布變換變成橢圓，所以此處測量的是平均半徑。

示例:

float radius = 100;
float result = 0;

// 構造一個matrix，x坐標縮放0.5
Matrix matrix = new Matrix();
matrix.setScale(0.5f, 1f);

Log.i(TAG, "mapRadius: "+radius);

result = matrix.mapRadius(radius);

Log.i(TAG, "mapRadius: "+result);

結果:

mapRadius: 100.0
mapRadius: 70.71068

3.mapRect

boolean mapRect (RectF rect)

boolean mapRect (RectF dst, RectF src)

測量矩形變換後位置。

(1) boolean mapRect (RectF rect) 測量rect並將測量結果放入rect中，返回值是判斷矩形經過變換後是否仍為矩形。

示例：

RectF rect = new RectF(400, 400, 1000, 800);

// 構造一個matrix
Matrix matrix = new Matrix();
matrix.setScale(0.5f, 1f);
matrix.postSkew(1,0);

Log.i(TAG, "mapRadius: "+rect.toString());

boolean result = matrix.mapRect(rect);

Log.i(TAG, "mapRadius: "+rect.toString());
Log.e(TAG, "isRect: "+ result);

結果：

mapRadius: RectF(400.0, 400.0, 1000.0, 800.0)
mapRadius: RectF(600.0, 400.0, 1300.0, 800.0)
isRect: false

>

由於使用了錯切，所以返回結果為false。

(2) boolean mapRect (RectF dst, RectF src) 測量src並將測量結果放入dst中，返回值是判斷矩形經過變換後是否仍為矩形,和之前沒有什麼太大區別，此處就不啰嗦了。

4.mapVectors

測量向量。

void mapVectors (float[] vecs)

void mapVectors (float[] dst, float[] src)

void mapVectors (float[] dst, int dstIndex, float[] src, int srcIndex, int vectorCount)

mapVectors 與 mapPoints 基本上是相同的，可以直接參照上面的mapPoints使用方法。

而兩者唯一的區別就是mapVectors不會受到位移的影響，這符合向量的定律，如果你不了解的話，請找到以前教過你的老師然後把學費要回來。

區別:

float[] src = new float[]{1000, 800};
float[] dst = new float[2];

// 構造一個matrix
Matrix matrix = new Matrix();
matrix.setScale(0.5f, 1f);
matrix.postTranslate(100,100);

// 計算向量, 不受位移影響
matrix.mapVectors(dst, src);
Log.i(TAG, "mapVectors: "+Arrays.toString(dst));

// 計算點
matrix.mapPoints(dst, src);
Log.i(TAG, "mapPoints: "+Arrays.toString(dst));

結果:

mapVectors: [500.0, 800.0]
mapPoints: [600.0, 900.0]

set、pre 與 post

對於四種基本變換 平移(translate)、縮放(scale)、旋轉(rotate)、 錯切(skew) 它們每一種都三種操作方法，分別為 設置(set)、 前乘(pre) 和 後乘 (post)。而它們的基礎是Concat，通過先構造出特殊矩陣然後用原始矩陣Concat特殊矩陣，達到變換的結果。

關於四種基本變換的知識和三種對應操作的區別，詳細可以參考 Canvas之畫布操作 和 Matrix原理 這兩篇文章的內容。

由於之前的文章已經詳細的講解過了它們的原理與用法，所以此處就簡要的介紹一下:

方法 簡介 set 設置，會覆蓋掉之前的數值，導致之前的操作失效。 pre 前乘，相當於矩陣的右乘， M' = M * S (S指為特殊矩陣) post 後乘，相當於矩陣的左乘，M' = S * M （S指為特殊矩陣）

Matrix 相關的重要知識：

1.一開始從Canvas中獲取到到Matrix並不是初始矩陣，而是經過偏移後到矩陣，且偏移距離就是距離屏幕左上角的位置。

這個可以用於判定View在屏幕上的絕對位置，View可以根據所處位置做出調整。

2.構造Matrix時使用的是矩陣乘法，前乘(pre)與後乘(post)結果差別很大。

這個直接參見上一篇文章 Matrix原理 即可。

3.受矩陣乘法影響，後面的執行的操作可能會影響到之前的操作。

使用時需要注意構造順序。

特殊方法

這一類方法看似不起眼，但拿來稍微加工一下就可能制作意想不到的效果。

1.setPolyToPoly

boolean setPolyToPoly (
        float[] src,    // 原始數組 src [x,y]，存儲內容為一組點
        int srcIndex,   // 原始數組開始位置
        float[] dst,    // 目標數組 dst [x,y]，存儲內容為一組點
        int dstIndex,   // 目標數組開始位置
        int pointCount) // 測控點的數量 取值范圍是: 0到4

Poly全稱是Polygon，多邊形的意思，了解了意思大致就能知道這個方法是做什麼用的了，應該與PS中自由變換中的扭曲有點類似。

vcejrL/J0tTNqLn91eLLxLj2vce9q8rTzby0077Y0M6x5Lu7s8nG5Mv70M7XtKGjPC9jb2RlPjwvY29kZT48L2NvZGU+PC9jb2RlPjwvY29kZT48L2NvZGU+PC9jb2RlPjwvY29kZT48L2NvZGU+PC9jb2RlPjwvY29kZT48L2NvZGU+PC9wPg0KPC9ibG9ja3F1b3RlPg0KPHA+vPK1pcq+wP06PC9jb2RlPjwvY29kZT48L2NvZGU+PC9jb2RlPjwvY29kZT48L2NvZGU+PC9jb2RlPjwvY29kZT48L2NvZGU+PC9jb2RlPjwvY29kZT48L2NvZGU+PC9wPg0KPHByZSBjbGFzcz0="brush:java;"> public class MatrixSetPolyToPolyTest extends View { private Bitmap mBitmap; // 要繪制的圖片 private Matrix mPolyMatrix; // 測試setPolyToPoly用的Matrix public MatrixSetPolyToPolyTest(Context context) { super(context); initBitmapAndMatrix(); } private void initBitmapAndMatrix() { mBitmap = BitmapFactory.decodeResource(getResources(), R.drawable.poly_test); mPolyMatrix = new Matrix(); float[] src = {0, 0, // 左上 mBitmap.getWidth(), 0, // 右上 mBitmap.getWidth(), mBitmap.getHeight(), // 右下 0, mBitmap.getHeight()}; // 左下 float[] dst = {0, 0, // 左上 mBitmap.getWidth(), 400, // 右上 mBitmap.getWidth(), mBitmap.getHeight() - 200, // 右下 0, mBitmap.getHeight()}; // 左下 // 核心要點 mPolyMatrix.setPolyToPoly(src, 0, dst, 0, src.length >> 1); // src.length >> 1 為位移運算 相當於處以2 // 此處為了更好的顯示對圖片進行了等比縮放和平移(圖片本身有點大) mPolyMatrix.postScale(0.26f, 0.26f); mPolyMatrix.postTranslate(0,200); } @Override protected void onDraw(Canvas canvas) { super.onDraw(canvas); // 根據Matrix繪制一個變換後的圖片 canvas.drawBitmap(mBitmap, mPolyMatrix, null); } }

文章發出後有小伙伴在GitHub上提出疑問，說此處講解到並不清楚，尤其是最後的一個參數，所以特此補充一下內容。

我們知道pointCount支持點的個數為0到4個，四個一般指圖形的四個角，屬於最常用的一種情形，但前面幾種是什麼情況呢？

發布此文的時候之所以沒有講解0到3的情況，是因為前面的幾種情況在實際開發中很少會出現， 才不是因為偷懶呢，哼。

pointCount 摘要 0 相當於reset 1 相當於translate 2 可以進行 縮放、旋轉、平移 變換 3 可以進行 縮放、旋轉、平移、錯切 變換 4 可以進行 縮放、旋轉、平移、錯切以及任何形變

從上表我們可以觀察出一個規律, 隨著pointCount數值增大setPolyToPoly的可以操作性也越來越強，這不是廢話麼，可調整點數多了能干的事情自然也多了。

只列一個表格就算交代完畢了顯得誠意不足，為了彰顯誠意，接下來詳細的講解一下。

為什麼說前面幾種情況在實際開發中很少出現?

作為開發人員，寫出來的代碼出了要讓機器”看懂”，沒有歧義之外，最重要的還是讓人看懂，以方便後期的維護修改，從上邊的表格中可以看出，前面的幾種種情況都可以有更直觀的替代方法，只有四個參數的情況下的特殊形變是沒有替代方法的。

測控點選取位置?

測控點可以選擇任何你認為方便的位置，只要src與dst一一對應即可。不過為了方便，通常會選擇一些特殊的點： 圖形的四個角，邊線的中心點以及圖形的中心點等。不過有一點需要注意，測控點選取都應當是不重復的(src與dst均是如此)，如果選取了重復的點會直接導致測量失效，這也意味著，你不允許將一個方形(四個點)映射為三角形(四個點，但其中兩個位置重疊)，但可以接近於三角形。。

作用范圍?

作用范圍當然是設置了Matrix的全部區域，如果你將這個Matrix賦值給了Canvas，它的作用范圍就是整個畫布，如果你賦值給了Bitmap，它的作用范圍就是整張圖片。

---

接下來用示例演示一下，所有示例的src均為圖片大小，dst根據手勢變化。

pointCount為0

pointCount為0和reset是等價的，而不是保持matrix不變，在最底層的實現中可以看到這樣的代碼：

if (0 == count) {
    this->reset();
    return true;
}

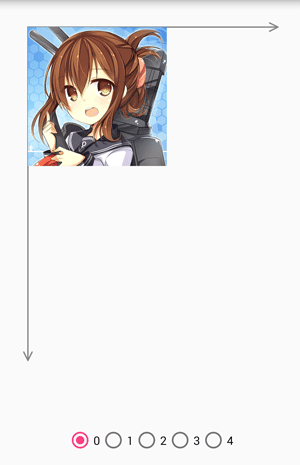
pointCount為1

pointCount為0和translate是等價的，在最底層的實現中可以看到這樣的代碼：

if (1 == count) {
    this->setTranslate(dst[0].fX - src[0].fX, dst[0].fY - src[0].fY);
    return true;
}

平移的距離是dst - src.

當測控點為1的時候，由於你只有一個點可以控制，所以你只能拖拽著它在2D平面上滑動。

pointCount為2

當pointCount為2的時候，可以做縮放、平移和旋轉。

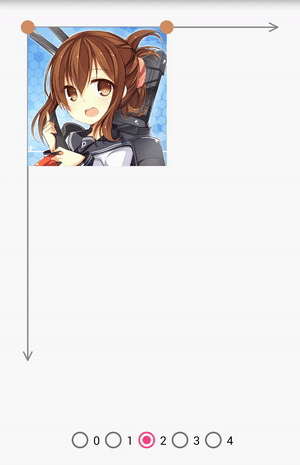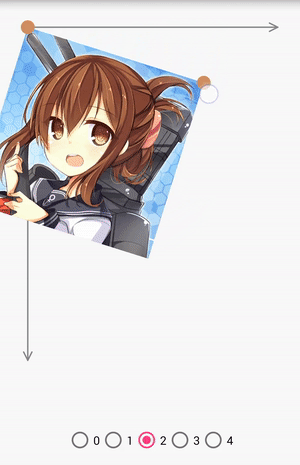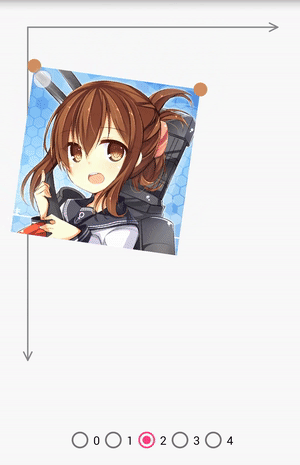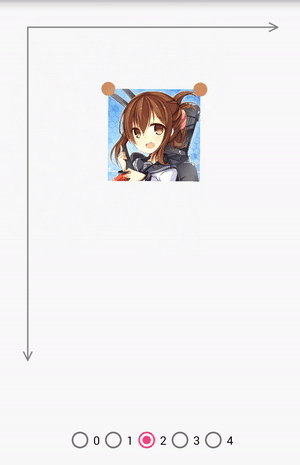
pointCount為3

當pointCount為3的時候，可以做縮放、平移、旋轉和錯切。

pointCount為4

當pointCount為4的時候，你可以將圖像拉伸為任意四邊形。

上面已經用圖例比較詳細的展示了不同操控點個數的情況，如果你依舊存在疑問，可以獲取代碼自己試一下。

AndroidNote/blob/master/CustomView/Advance/Code/SetPolyToPoly.md" target="_blank">點擊此處查看setPolyToPoly測試代碼

2.setRectToRect

boolean setRectToRect (RectF src,           // 源區域
                RectF dst,                  // 目標區域
                Matrix.ScaleToFit stf)      // 縮放適配模式

簡單來說就是將源矩形的內容填充到目標矩形中，然而在大多數的情況下，源矩形和目標矩形的長寬比是不一致的，到底該如何填充呢，這個填充的模式就由第三個參數 stf 來確定。

ScaleToFit 是一個枚舉類型，共包含了四種模式:

模式 摘要 CENTER 居中，對src等比例縮放，將其居中放置在dst中。 START 頂部，對src等比例縮放，將其放置在dst的左上角。 END 底部，對src等比例縮放，將其放置在dst的右下角。 FILL 充滿，拉伸src的寬和高，使其完全填充滿dst。

下面我們看一下不同寬高比的src與dst在不同模式下是怎樣的。

假設灰色部分是dst，橙色部分是src，由於是測試不同寬高比，示例中讓dst保持不變，看兩種寬高比的src在不同模式下填充的位置。

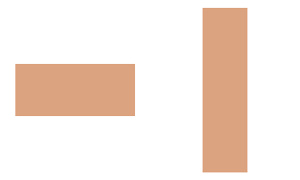
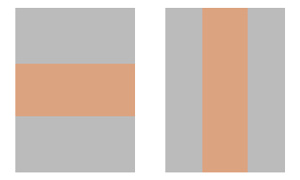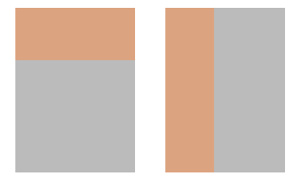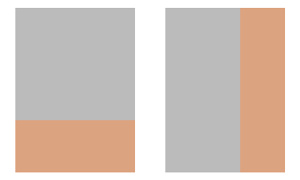src(原始狀態) CENTER START END FILL

下面用代碼演示一下居中的示例:

public class MatrixSetRectToRectTest extends View {

    private static final String TAG = "MatrixSetRectToRectTest";

    private int mViewWidth, mViewHeight;

    private Bitmap mBitmap;             // 要繪制的圖片
    private Matrix mRectMatrix;         // 測試etRectToRect用的Matrix

    public MatrixSetRectToRectTest(Context context) {
        super(context);

        mBitmap = BitmapFactory.decodeResource(getResources(), R.drawable.rect_test);
        mRectMatrix = new Matrix();
    }

    @Override
    protected void onSizeChanged(int w, int h, int oldw, int oldh) {
        super.onSizeChanged(w, h, oldw, oldh);
        mViewWidth = w;
        mViewHeight = h;

    }

    @Override
    protected void onDraw(Canvas canvas) {
        super.onDraw(canvas);

        RectF src= new RectF(0, 0, mBitmap.getWidth(), mBitmap.getHeight() );
        RectF dst = new RectF(0, 0, mViewWidth, mViewHeight );

        // 核心要點
        mRectMatrix.setRectToRect(src,dst, Matrix.ScaleToFit.CENTER);

        // 根據Matrix繪制一個變換後的圖片
        canvas.drawBitmap(mBitmap, mRectMatrix, new Paint());
    }
}

3.rectStaysRect

判斷矩形經過變換後是否仍為矩形，假如Matrix進行了平移、縮放則畫布僅僅是位置和大小改變，矩形變換後仍然為矩形，但Matrix進行了非90度倍數的旋轉或者錯切，則矩形變換後就不再是矩形了，這個很好理解，不過多贅述，順便說一下，前面的mapRect方法的返回值就是根據rectStaysRect來判斷的。

4.setSinCos

設置sinCos值，這個是控制Matrix旋轉的，由於Matrix已經封裝好了Rotate方法，所以這個並不常用，在此僅作概述。

// 方法一
void setSinCos (float sinValue,     // 旋轉角度的sin值
                float cosValue)     // 旋轉角度的cos值

// 方法二
void setSinCos (float sinValue,     // 旋轉角度的sin值
                float cosValue,     // 旋轉角度的cos值
                float px,           // 中心位置x坐標
                float py)           // 中心位置y坐標

簡單測試:

Matrix matrix = new Matrix();
// 旋轉90度
// sin90=1
// cos90=0
matrix.setSinCos(1f, 0f);

Log.i(TAG, "setSinCos:"+matrix.toShortString());

// 重置
matrix.reset();

// 旋轉90度
matrix.setRotate(90);

Log.i(TAG, "setRotate:"+matrix.toShortString());

結果:

setSinCos:[0.0, -1.0, 0.0][1.0, 0.0, 0.0][0.0, 0.0, 1.0]
setRotate:[0.0, -1.0, 0.0][1.0, 0.0, 0.0][0.0, 0.0, 1.0]

矩陣相關

矩陣相關的函數就屬於哪一種非常靠近底層的東西了，大部分開發者很少直接接觸這些東西，想要弄明白這個可以回去請教你們的線性代數老師，這裡也僅作概述。

方法 摘要 invert 求矩陣的逆矩陣 isAffine 判斷當前矩陣是否為仿射矩陣，API21(5.0)才添加的方法。 isIdentity 判斷當前矩陣是否為單位矩陣。

1.invert

求矩陣的逆矩陣，簡而言之就是計算與之前相反的矩陣，如果之前是平移200px，則求的矩陣為反向平移200px，如果之前是縮小到0.5f，則結果是放大到2倍。

boolean invert (Matrix inverse)

簡單測試:

Matrix matrix = new Matrix();
Matrix invert = new Matrix();
matrix.setTranslate(200,500);

Log.e(TAG, "before - matrix "+matrix.toShortString() );

Boolean result = matrix.invert(invert);

Log.e(TAG, "after  - result "+result );
Log.e(TAG, "after  - matrix "+matrix.toShortString() );
Log.e(TAG, "after  - invert "+invert.toShortString() );

結果：

before - matrix [1.0, 0.0, 200.0][0.0, 1.0, 500.0][0.0, 0.0, 1.0]
after  - result true
after  - matrix [1.0, 0.0, 200.0][0.0, 1.0, 500.0][0.0, 0.0, 1.0]
after  - invert [1.0, 0.0, -200.0][0.0, 1.0, -500.0][0.0, 0.0, 1.0]

2.isAffine

判斷矩陣是否是仿射矩陣, 貌似並沒有太大卵用，因為你無論如何操作結果始終都為true。

這是為什麼呢？因為迄今為止我們使用的所有變換都是仿射變換，那變換出來的矩陣自然是仿射矩陣喽。

判斷是否是仿射矩陣最重要的一點就是，直線是否仍為直線，簡單想一下就知道，不論平移，旋轉，錯切，縮放，直線變換後最終仍為直線，要想讓isAffine的結果變為false，除非你能把直線掰彎，我目前還沒有找到能夠掰彎的方法，所以我仍是直男(就算找到了，我依舊是直男)。

簡單測試:

Matrix matrix = new Matrix();
Log.i(TAG,"isAffine="+matrix.isAffine());

matrix.postTranslate(200,0);
matrix.postScale(0.5f, 1);
matrix.postSkew(0,1);
matrix.postRotate(56);

Log.i(TAG,"isAffine="+matrix.isAffine());

結果:

isAffine=true
isAffine=true

3.isIdentity

判斷是否為單位矩陣，什麼是單位矩陣呢，就是文章一開始的那個:

新創建的Matrix和重置後的Matrix都是單位矩陣，不過，只要隨意操作一步，就不在是單位矩陣了。

簡單測試：

Matrix matrix = new Matrix();
Log.i(TAG,"isIdentity="+matrix.isIdentity());

matrix.postTranslate(200,0);

Log.i(TAG,"isIdentity="+matrix.isIdentity());

結果：

isIdentity=true
isIdentity=false

Matrix實用技巧

通過前面的代碼和示例，我們已經了解了Matrix大部分方法是如何使用的，這些基本的原理和方法通過組合可能會創造出神奇的東西，網上有很多教程講Bitmap利用Matrix變換來制作鏡像倒影等，這都屬於Matrix的基本應用，我就不在贅述了，下面我簡要介紹幾種然並卵的小技巧，更多的大家可以開啟自己的腦洞來發揮。

1.獲取View在屏幕上的絕對位置

在之前的文章Matrix原理中我們提到過Matrix最根本的作用就是坐標映射，將View的相對坐標映射為屏幕的絕對坐標，也提到過我們在onDraw函數的canvas中獲取到到Matrix並不是單位矩陣，結合這兩點，聰明的你肯定想到了我們可以從canvas的Matrix入手取得View在屏幕上的絕對位置。

不過，這也僅僅是一個然並卵的小技巧而已，使用getLocationOnScreen同樣可以獲取View在屏幕的位置，但如果你是想讓下一任接盤俠弄不明白你在做什麼或者是被同事打死的話，盡管這麼做。

簡單示例:

@Override
protected void onDraw(Canvas canvas) {
    float[] values = new float[9];
    int[] location1 = new int[2];

    Matrix matrix = canvas.getMatrix();
    matrix.getValues(values);

    location1[0] = (int) values[2];
    location1[1] = (int) values[5];
    Log.i(TAG, "location1 = " + Arrays.toString(location1));

    int[] location2 = new int[2];
    this.getLocationOnScreen(location2);
    Log.i(TAG, "location2 = " + Arrays.toString(location2));
}

結果:

location1 = [0, 243]
location2 = [0, 243]

2.利用setPolyToPoly制造3D效果

這個全憑大家想象力啦，不過我搜了一下還真搜到了好東西，之前鴻洋大大發過一篇博文詳細講解了利用setPolyToPoly制造的折疊效果布局，大家直接到他的博客去看吧，我就不寫了。

圖片引用自鴻洋大大的博客，稍作了一下處理。

總結

本篇基本講解了Matrix相關的所有方法，應該是目前對Matrix講解最全面的一篇中文文章了，建議配合上一篇Matrix原理食用效果更佳。

由於本人水平有限，可能出於誤解或者筆誤難免出錯，如果發現有問題或者對文中內容存在疑問歡迎在下面評論區告訴我，請對問題描述盡量詳細，以幫助我可以快速找到問題根源。