編輯:關於Android編程
從去年開始了解貝塞爾曲線之後,發現開發中,不管是Android/Ios平台,還是web前端等,都有貝塞爾曲線的應用,通過繪制貝塞爾曲線,可以幫助開發者實現很多效果,例如一段時間內很流行的粘合型的下拉刷新、又如天氣曲線圖,同時,以貝塞爾曲線為基礎的貝塞爾工具是所有繪圖軟件的最常用最實用的工具。
貝塞爾曲線(Béziercurve),又稱貝茲曲線或貝濟埃曲線,是應用於二維圖形應用程序的數學曲線。一般的矢量圖形軟件通過它來精確畫出曲線,貝茲曲線由線段與節點組成,節點是可拖動的支點,線段像可伸縮的皮筋,我們在繪圖工具上看到的鋼筆工具就是來做這種矢量曲線的。主要結構:起始點、終止點(也稱錨點)、控制點。通過調整控制點,貝塞爾曲線的形狀會發生變化。
一階貝塞爾曲線(線段):
公式:
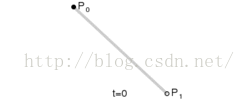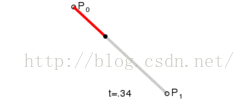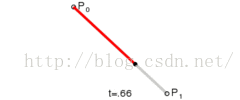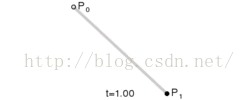
意義:由P0至P1的連續點,描述的一條線段
二階貝塞爾曲線(拋物線):
公式:
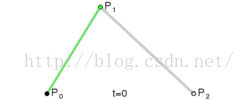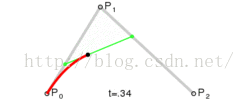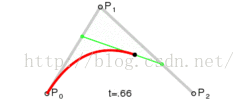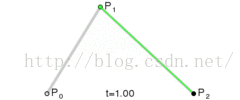
原理:由P0至P1的連續點Q0,描述一條線段。
由P1至P2的連續點Q1,描述一條線段。
由Q0至Q1的連續點B(t),描述一條二次貝塞爾曲線。
三階貝塞爾曲線:

當然還有四階曲線、五階曲線......
一篇幫助理解貝塞爾曲線的文章:http://www.html-js.com/article/1628
一個幫助繪制貝塞爾曲線的網址:http://bezier.method.ac/
我們一般使用的是二階貝塞爾曲線和三階貝塞爾曲線,從動態圖和公式我們可以看出,貝塞爾曲線主要由於三個部分控制:起點,終點,中間的輔助控制點。如何利用這三個點畫出貝塞爾曲線,在android自帶的Path類中自帶了方法,可以幫助我們實現貝塞爾曲線:
/**
* Add a quadratic bezier from the last point, approaching control point
* (x1,y1), and ending at (x2,y2). If no moveTo() call has been made for
* this contour, the first point is automatically set to (0,0).
*
* @param x1 The x-coordinate of the control point on a quadratic curve
* @param y1 The y-coordinate of the control point on a quadratic curve
* @param x2 The x-coordinate of the end point on a quadratic curve
* @param y2 The y-coordinate of the end point on a quadratic curve
*/
public void quadTo(float x1, float y1, float x2, float y2) {
isSimplePath = false;
native_quadTo(mNativePath, x1, y1, x2, y2);
}
quadTo()方法從上一個點為起點開始繪制貝塞爾曲線,其中(x1,y1)為輔助控制點,(x2,y2)為終點。
PathmPath=newPath();
mPath.moveTo(x0,y0);
mPath.quadTo(x1,y1,x2,y2);
如調用以上代碼,即繪制起點(x0,y0),終點(x2,y2),輔助控制點(x1,y1)的貝塞爾曲線。因此,通過不斷改變這三個點的位置,我們可以繪制出各種各樣的曲線
/**
* Add a cubic bezier from the last point, approaching control points
* (x1,y1) and (x2,y2), and ending at (x3,y3). If no moveTo() call has been
* made for this contour, the first point is automatically set to (0,0).
*
* @param x1 The x-coordinate of the 1st control point on a cubic curve
* @param y1 The y-coordinate of the 1st control point on a cubic curve
* @param x2 The x-coordinate of the 2nd control point on a cubic curve
* @param y2 The y-coordinate of the 2nd control point on a cubic curve
* @param x3 The x-coordinate of the end point on a cubic curve
* @param y3 The y-coordinate of the end point on a cubic curve
*/
public void cubicTo(float x1, float y1, float x2, float y2,
float x3, float y3) {
isSimplePath = false;
native_cubicTo(mNativePath, x1, y1, x2, y2, x3, y3);
}
cubicTo()方法從上一個點為起點開始繪制三階貝塞爾曲線,其中(x1,y1),(x2,y2)為輔助控制點,(x3,y3)為終點。
(1)二階貝塞爾曲線——波浪
要實現一個波浪不斷湧動的效果,這種效果在很多手機應用中可見,例如手機電量,內存剩余等。我們需要繪制帶有平滑自然效果的曲線,這時候就需要貝塞爾曲線來輔助了。
動態圖:

原理圖:
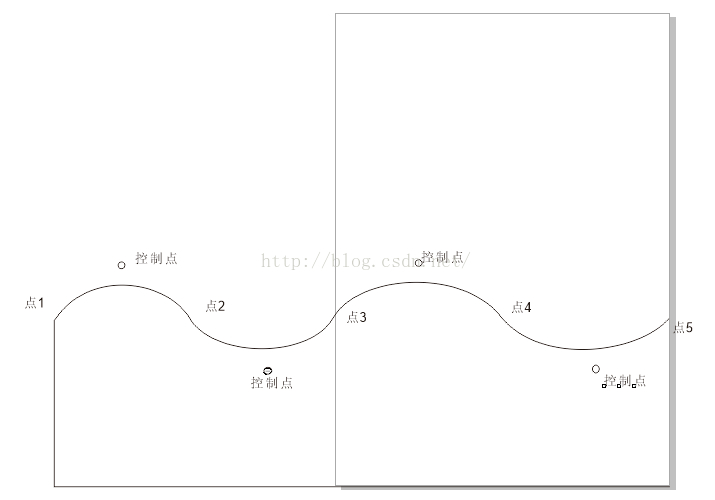
圖中的矩陣即為視圖的可見范圍,也就是我們手機常見的區域。通過屬性動畫類ValueAnimator不斷改變點1的橫坐標,隨著點1橫坐標向右移動,點2,點3,點4,點5,以及四個控制點的坐標隨著點1的移動同時位移相同距離,每一次坐標點更新,我們調用一次invalidate()方法,調用draw重新繪制視圖,繪制四段貝塞爾曲線。最後點1移動到原先點3的位置,這樣就完成了一次動畫。
這樣,通過循環不斷的動畫效果,我們就實現了波浪的效果。
onDraw() 代碼:
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
if (!mIsRunning || !mHasInit)
return;
mPath.reset();
mPath.moveTo(mLeft1.x, mLeft1.y);
mPath.quadTo(mControlLeft1.x, mControlLeft1.y, mLeft2.x, mLeft2.y);
mPath.quadTo(mControlLeft2.x, mControlLeft2.y, mFirst.x, mFirst.y);
mPath.quadTo(mControlFirst.x, mControlFirst.y, mSecond.x, mSecond.y);
mPath.quadTo(mControlSecond.x, mControlSecond.y, mRight.x, mRight.y);
mPath.lineTo(mRight.x, mHeight);
mPath.lineTo(mLeft1.x, mHeight);
mPath.lineTo(mLeft1.x, mLeft1.y);
canvas.drawPath(mPath, mPaint);
}
(2)二階貝塞爾曲線——粘連體
利用二階貝塞爾曲線還可以實現,類似兩種物體粘合在一起的效果,比如我們常用的qq,在qq聊天列表上有一個非常有意思的功能,就是當我們用手指移動聊天列表上的未讀消息標志的時候,它與聊天列表會產生粘連的效果:
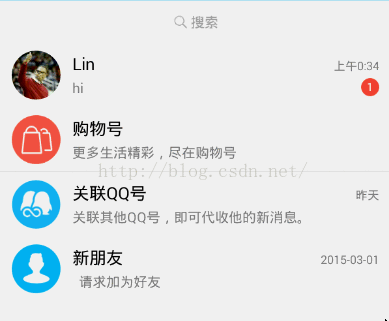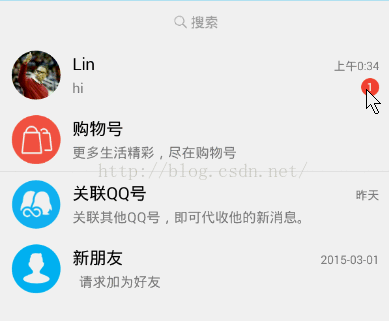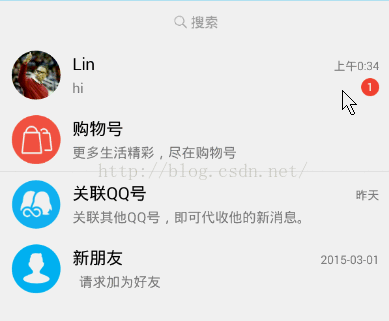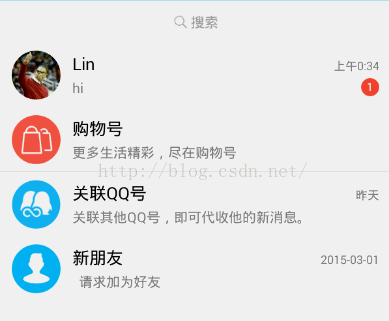
現在,我們來模擬這種效果,利用學到的二階貝塞爾曲線來繪制。
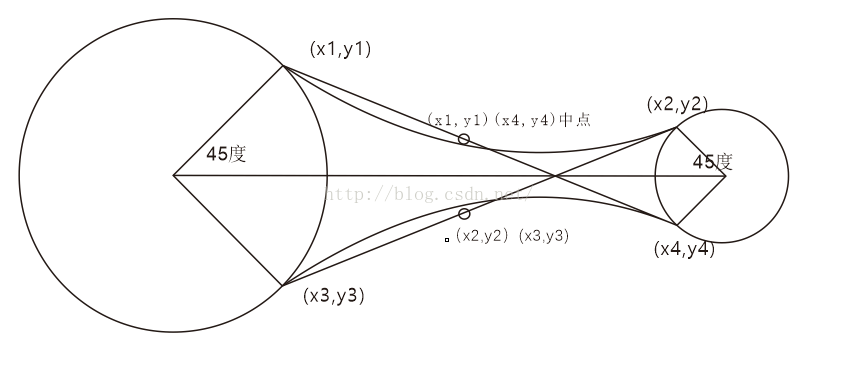
我們看到原理圖,基本構造為兩個圓,和兩端貝塞爾曲線,繪制貝塞爾曲線,由於這是一個二階的貝塞爾曲線,我們只需要一個控制點,在這個圖裡,我們的兩條貝塞爾曲線的兩個控制點分別為(x1,y1)(x4,y4)的中點,(x2,y2)(x3,y3)的中點。
從圖中可以看出,我們的貝塞爾曲線由我們的控制點控制,控制點又是被起點和終點控制著,因此,當兩個圓距離越大,曲線越趨於平緩,當兩個圓距離越小,曲線的波動度越大,這樣,我們想要的粘連的效果就實現了。另外,這裡有一個還有角度(圖中的45度角)可以用來控制,也可以作為控制曲線波動度的參數。
通過以上分析,我們通過一個方法來繪制兩個圓之間的粘連體路徑:
/**
* 畫粘連體
* @param cx1 圓心x1
* @param cy1 圓心y1
* @param r1 圓半徑r1
* @param offset1 貝塞爾曲線偏移角度offset1
* @param cx2 圓心x2
* @param cy2 圓心y2
* @param r2 圓半徑r2
* @param offset2 貝塞爾曲線偏移角度offset2
* @return
*/
public static Path drawAdhesionBody(float cx1, float cy1, float r1, float offset1, float
cx2, float cy2, float r2, float offset2) {
/* 求三角函數 */
float degrees =(float) Math.toDegrees(Math.atan(Math.abs(cy2 - cy1) / Math.abs(cx2 - cx1)));
/* 根據圓1與圓2的相對位置求四個點 */
float differenceX = cx1 - cx2;
float differenceY = cy1 - cy2;
/* 兩條貝塞爾曲線的四個端點 */
float x1,y1,x2,y2,x3,y3,x4,y4;
/* 圓1在圓2的下邊 */
if (differenceX == 0 && differenceY > 0) {
x2 = cx2 - r2 * (float) Math.sin(Math.toRadians(offset2));
y2 = cy2 + r2 * (float) Math.cos(Math.toRadians(offset2));
x4 = cx2 + r2 * (float) Math.sin(Math.toRadians(offset2));
y4 = cy2 + r2 * (float) Math.cos(Math.toRadians(offset2));
x1 = cx1 - r1 * (float) Math.sin(Math.toRadians(offset1));
y1 = cy1 - r1 * (float) Math.cos(Math.toRadians(offset1));
x3 = cx1 + r1 * (float) Math.sin(Math.toRadians(offset1));
y3 = cy1 - r1 * (float) Math.cos(Math.toRadians(offset1));
}
/* 圓1在圓2的上邊 */
else if (differenceX == 0 && differenceY < 0) {
x2 = cx2 - r2 * (float) Math.sin(Math.toRadians(offset2));
y2 = cy2 - r2 * (float) Math.cos(Math.toRadians(offset2));
x4 = cx2 + r2 * (float) Math.sin(Math.toRadians(offset2));
y4 = cy2 - r2 * (float) Math.cos(Math.toRadians(offset2));
x1 = cx1 - r1 * (float) Math.sin(Math.toRadians(offset1));
y1 = cy1 + r1 * (float) Math.cos(Math.toRadians(offset1));
x3 = cx1 + r1 * (float) Math.sin(Math.toRadians(offset1));
y3 = cy1 + r1 * (float) Math.cos(Math.toRadians(offset1));
}
/* 圓1在圓2的右邊 */
else if (differenceX > 0 && differenceY == 0) {
x2 = cx2 + r2 * (float) Math.cos(Math.toRadians(offset2));
y2 = cy2 + r2 * (float) Math.sin(Math.toRadians(offset2));
x4 = cx2 + r2 * (float) Math.cos(Math.toRadians(offset2));
y4 = cy2 - r2 * (float) Math.sin(Math.toRadians(offset2));
x1 = cx1 - r1 * (float) Math.cos(Math.toRadians(offset1));
y1 = cy1 + r1 * (float) Math.sin(Math.toRadians(offset1));
x3 = cx1 - r1 * (float) Math.cos(Math.toRadians(offset1));
y3 = cy1 - r1 * (float) Math.sin(Math.toRadians(offset1));
}
/* 圓1在圓2的左邊 */
else if (differenceX < 0 && differenceY == 0 ) {
x2 = cx2 - r2 * (float) Math.cos(Math.toRadians(offset2));
y2 = cy2 + r2 * (float) Math.sin(Math.toRadians(offset2));
x4 = cx2 - r2 * (float) Math.cos(Math.toRadians(offset2));
y4 = cy2 - r2 * (float) Math.sin(Math.toRadians(offset2));
x1 = cx1 + r1 * (float) Math.cos(Math.toRadians(offset1));
y1 = cy1 + r1 * (float) Math.sin(Math.toRadians(offset1));
x3 = cx1 + r1 * (float) Math.cos(Math.toRadians(offset1));
y3 = cy1 - r1 * (float) Math.sin(Math.toRadians(offset1));
}
/* 圓1在圓2的右下角 */
else if (differenceX > 0 && differenceY > 0) {
x2 = cx2 - r2 * (float) Math.cos(Math.toRadians(180 - offset2 - degrees));
y2 = cy2 + r2 * (float) Math.sin(Math.toRadians(180 - offset2 - degrees));
x4 = cx2 + r2 * (float) Math.cos(Math.toRadians(degrees - offset2));
y4 = cy2 + r2 * (float) Math.sin(Math.toRadians(degrees - offset2));
x1 = cx1 - r1 * (float) Math.cos(Math.toRadians(degrees - offset1));
y1 = cy1 - r1 * (float) Math.sin(Math.toRadians(degrees - offset1));
x3 = cx1 + r1 * (float) Math.cos(Math.toRadians(180 - offset1 - degrees));
y3 = cy1 - r1 * (float) Math.sin(Math.toRadians(180 - offset1 - degrees));
}
/* 圓1在圓2的左上角 */
else if (differenceX < 0 && differenceY < 0) {
x2 = cx2 - r2 * (float) Math.cos(Math.toRadians(degrees - offset2));
y2 = cy2 - r2 * (float) Math.sin(Math.toRadians(degrees - offset2));
x4 = cx2 + r2 * (float) Math.cos(Math.toRadians(180 - offset2 - degrees));
y4 = cy2 - r2 * (float) Math.sin(Math.toRadians(180 - offset2 - degrees));
x1 = cx1 - r1 * (float) Math.cos(Math.toRadians(180 - offset1 - degrees));
y1 = cy1 + r1 * (float) Math.sin(Math.toRadians(180 - offset1 - degrees));
x3 = cx1 + r1 * (float) Math.cos(Math.toRadians(degrees - offset1));
y3 = cy1 + r1 * (float) Math.sin(Math.toRadians(degrees - offset1));
}
/* 圓1在圓2的左下角 */
else if (differenceX < 0 && differenceY > 0) {
x2 = cx2 - r2 * (float) Math.cos(Math.toRadians(degrees - offset2));
y2 = cy2 + r2 * (float) Math.sin(Math.toRadians(degrees - offset2));
x4 = cx2 + r2 * (float) Math.cos(Math.toRadians(180 - offset2 - degrees));
y4 = cy2 + r2 * (float) Math.sin(Math.toRadians(180 - offset2 - degrees));
x1 = cx1 - r1 * (float) Math.cos(Math.toRadians(180 - offset1 - degrees));
y1 = cy1 - r1 * (float) Math.sin(Math.toRadians(180 - offset1 - degrees));
x3 = cx1 + r1 * (float) Math.cos(Math.toRadians(degrees - offset1));
y3 = cy1 - r1 * (float) Math.sin(Math.toRadians(degrees - offset1));
}
/* 圓1在圓2的右上角 */
else {
x2 = cx2 - r2 * (float) Math.cos(Math.toRadians(180 - offset2 - degrees));
y2 = cy2 - r2 * (float) Math.sin(Math.toRadians(180 - offset2 - degrees));
x4 = cx2 + r2 * (float) Math.cos(Math.toRadians(degrees - offset2));
y4 = cy2 - r2 * (float) Math.sin(Math.toRadians(degrees - offset2));
x1 = cx1 - r1 * (float) Math.cos(Math.toRadians(degrees - offset1));
y1 = cy1 + r1* (float) Math.sin(Math.toRadians(degrees - offset1));
x3 = cx1 + r1 * (float) Math.cos(Math.toRadians(180 - offset1 - degrees));
y3 = cy1 + r1 * (float) Math.sin(Math.toRadians(180 - offset1 - degrees));
}
/* 貝塞爾曲線的控制點 */
float anchorX1,anchorY1,anchorX2,anchorY2;
/* 圓1大於圓2 */
if (r1 > r2) {
anchorX1 = (x2 + x3) / 2;
anchorY1 = (y2 + y3) / 2;
anchorX2 = (x1 + x4) / 2;
anchorY2 = (y1 + y4) / 2;
}
/* 圓1小於或等於圓2 */
else {
anchorX1 = (x1 + x4) / 2;
anchorY1 = (y1 + y4) / 2;
anchorX2 = (x2 + x3) / 2;
anchorY2 = (y2 + y3) / 2;
}
/* 畫粘連體 */
Path path = new Path();
path.reset();
path.moveTo(x1, y1);
path.quadTo(anchorX1, anchorY1, x2, y2);
path.lineTo(x4, y4);
path.quadTo(anchorX2, anchorY2, x3, y3);
path.lineTo(x1, y1);
return path;
}
再來看仿QQ聊天列表的粘連效果,我們已經實現了粘連體的繪制,接下來,我們需要實現以上的基本效果,我們給控件設置一個粘連的最大距離,即如果兩個圓之間的距離超過這個值,則不再繪制粘連體。
好了,我們看效果圖:
粘連體除了在類似QQ上這種效果,其實還可以做很多事,比如,如果我們用它來實現一個加載頁面的效果呢。


(3)三階貝塞爾曲線——彈性球
三階貝塞爾曲線,就是有兩個控制點,公式太復雜,我也不是很理解,不過通過之前給出的那個網址來理解,還是比較好明白的,它相比二階曲線的優點是,由於控制點的增加,它能夠更加輕松地繪制出更平滑更自然的曲線。
先來看一個web前端的效果:
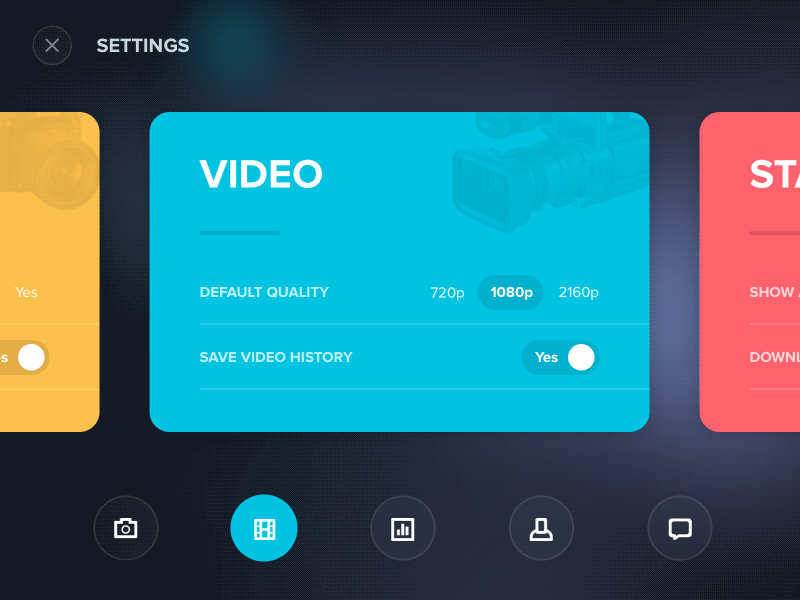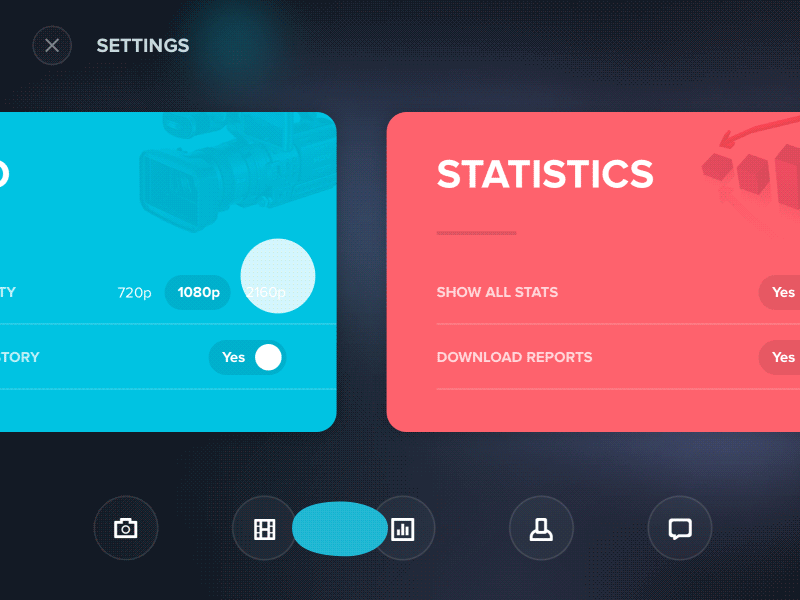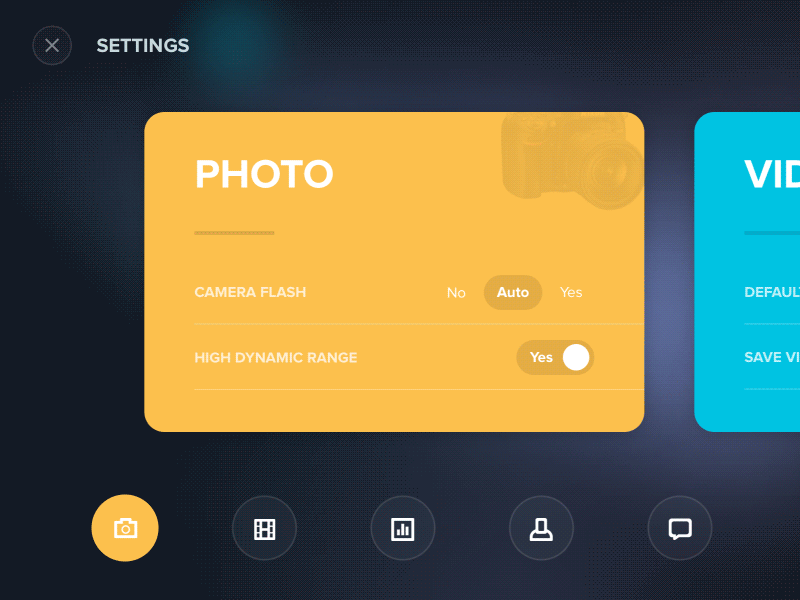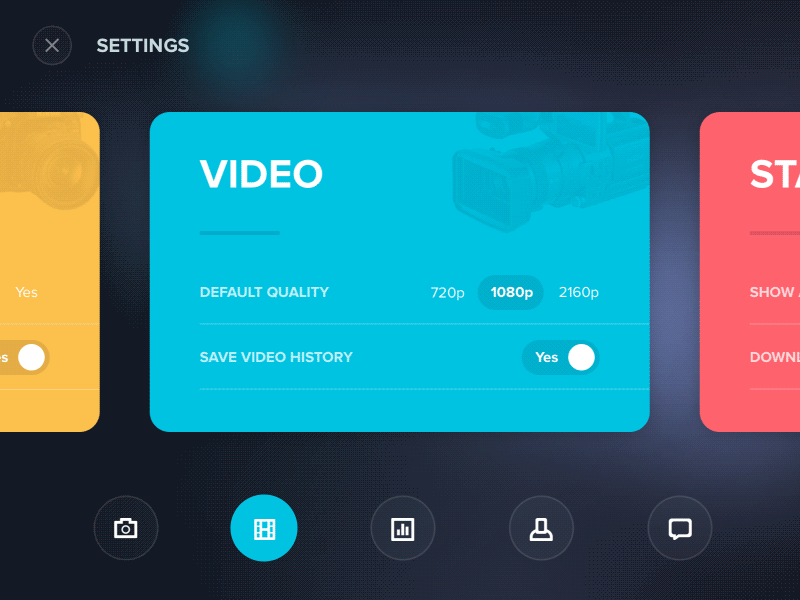
真的是很酷炫......
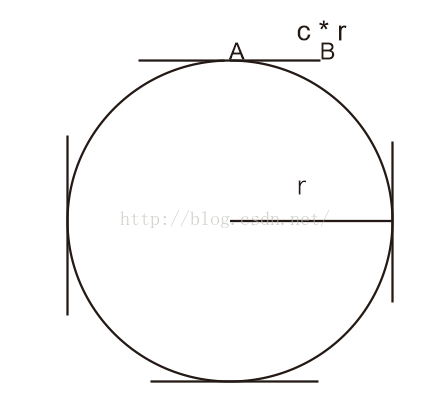
如何繪制類似這種,看起來具有彈性球的滑動球,我們需要使用三階貝塞爾曲線,那麼首先如何用三階貝塞爾曲線繪制出一個圓,這裡有一篇文章,是關於如何用貝塞爾曲線繪制圓:http://spencermortensen.com/articles/bezier-circle/,大概意思是講,我們需要一個值就是c=0.552284749,如下圖,要繪制右上角的圓弧,我們需要兩個控制點,其中B就是一個控制點,我們需要保證AB=c*r,即可以畫出1/4的圓弧,以此類推,連續畫四段這樣的圓弧,就可以畫出一個標准的圓。
接下來我們觀察彈性球的運動,大概可以分為以下幾個階段:
1)開始啟動,此時右邊點位移,其他點不動
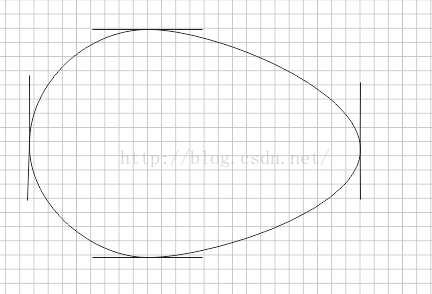
2)開始加速
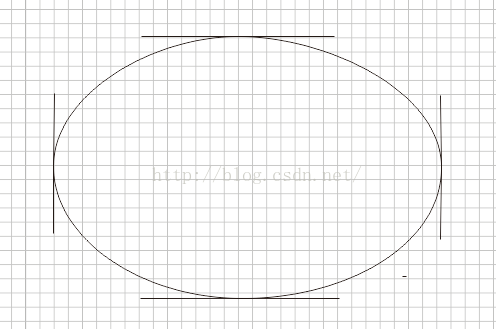
3)減速
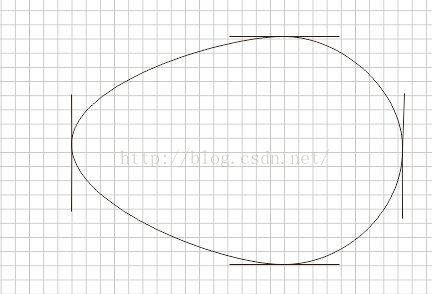
4)到達終點
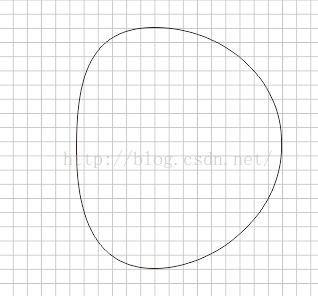
5)回彈效果
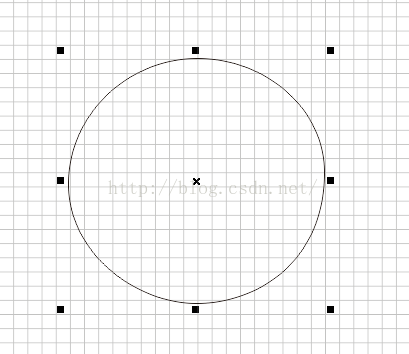
彈性球代碼:
package com.zero.bezier.widget.elastic;
import android.animation.Animator;
import android.animation.ValueAnimator;
import android.graphics.Path;
import android.graphics.PointF;
import android.view.animation.AccelerateDecelerateInterpolator;
/**
* 彈性球
* @author linzewu
* @date 2016/6/1
*/
public class ElasticBall extends Ball {
/**
* 向上運動
*/
private static final int DIRECTION_UP = 1;
/**
* 向下運動
*/
private static final int DIRECTION_DOWN = 2;
/**
* 向左運動
*/
private static final int DIRECTION_LEFT = 3;
/**
* 向右運動
*/
private static final int DIRECTION_RIGHT = 4;
/**
* 運動方向
*/
private int mDirection;
/**
* 動畫完成百分比(0~1)
*/
private float mAnimPercent;
/**
* 彈性距離
*/
private float mElasticDistance;
/**
* 彈性比例
*/
private float mElasticPercent = 0.8f;
/**
* 位移距離
*/
private float mMoveDistance;
/**
* 動畫消費時間
*/
private long mDuration = 1500;
/**
* 偏移值
*/
private float offsetTop, offsetBottom, offsetLeft, offsetRight;
/**
* 圓形偏移比例
*/
private float c = 0.551915024494f;
private float c2 = 0.65f;
/**
* 動畫開始點
*/
private Ball mStartPoint;
/**
* 動畫結束點
*/
private Ball mEndPoint;
/**
* 構造方法
*
* @param x 圓心橫坐標
* @param y 圓心縱坐標
* @param radius 圓半徑
*/
public ElasticBall(float x, float y, float radius) {
super(x, y, radius);
init();
}
private void init() {
mElasticDistance = mElasticPercent * radius;
offsetTop = c * radius;
offsetBottom = c * radius;
offsetLeft = c * radius;
offsetRight = c * radius;
}
public interface ElasticBallInterface{
void onChange(Path path);
void onFinish();
}
private ElasticBallInterface mElasticBallInterface;
/**
* 對外公布方法,設置彈性比例 (0~1)
* @param elasticPercent
*/
public void setElasticPercent(float elasticPercent) {
}
/**
* 對外公布方法,設置動畫時間
* @param duration
*/
public void setDuration(long duration) {
this.mDuration = duration;
}
/**
* 對外公布方法, 開啟動畫
* @param endPoint
*/
public void startElasticAnim(PointF endPoint, ElasticBallInterface elasticBallInterface) {
this.mEndPoint = new ElasticBall(endPoint.x, endPoint.y, radius);
this.mStartPoint = new ElasticBall(x, y, radius);
this.mStatusPoint1 = new ElasticBall(x, y, radius);
this.mStatusPoint2 = new ElasticBall(x, y, radius);
this.mStatusPoint3 = new ElasticBall(x, y, radius);
this.mStatusPoint4 = new ElasticBall(x, y, radius);
this.mStatusPoint5 = new ElasticBall(x, y, radius);
this.mElasticBallInterface = elasticBallInterface;
judgeDirection();
mMoveDistance = getDistance(mStartPoint.x, mStatusPoint1.y, endPoint.x, endPoint.y);
animStatus0();
ValueAnimator valueAnimator = ValueAnimator.ofFloat(0, 1);
valueAnimator.setDuration(mDuration);
valueAnimator.setInterpolator(new AccelerateDecelerateInterpolator());
valueAnimator.start();
valueAnimator.addUpdateListener(new ValueAnimator.AnimatorUpdateListener() {
@Override
public void onAnimationUpdate(ValueAnimator animation) {
mAnimPercent = (float) animation.getAnimatedValue();
if(mAnimPercent>=0 && mAnimPercent <= 0.2){
animStatus1();
}
else if(mAnimPercent > 0.2 && mAnimPercent <= 0.5){
animStatus2();
}
else if(mAnimPercent > 0.5 && mAnimPercent <= 0.8){
animStatus3();
}
else if(mAnimPercent > 0.8 && mAnimPercent <= 0.9){
animStatus4();
}
else if(mAnimPercent > 0.9&&mAnimPercent <= 1){
animStatus5();
}
if (mElasticBallInterface != null) {
mElasticBallInterface.onChange(drawElasticCircle(topX, topY, offsetTop, offsetTop,
bottomX, bottomY, offsetBottom, offsetBottom,
leftX, leftY, offsetLeft, offsetLeft,
rightX, rightY, offsetRight, offsetRight));
}
}
});
valueAnimator.addListener(new Animator.AnimatorListener() {
@Override
public void onAnimationStart(Animator animation) {
}
@Override
public void onAnimationEnd(Animator animation) {
if (mElasticBallInterface != null) {
mElasticBallInterface.onFinish();
}
}
@Override
public void onAnimationCancel(Animator animation) {
}
@Override
public void onAnimationRepeat(Animator animation) {
}
});
}
private void judgeDirection() {
if (mEndPoint.x - mStartPoint.x > 0) {
mDirection = DIRECTION_RIGHT;
}else if (mEndPoint.x - mStartPoint.x < 0) {
mDirection = DIRECTION_LEFT;
}else if (mEndPoint.y - mStartPoint.x > 0) {
mDirection = DIRECTION_DOWN;
}else if (mEndPoint.y - mStartPoint.y < 0){
mDirection = DIRECTION_UP;
}
}
/**
* 動畫狀態0 (初始狀態:圓形)
*/
private void animStatus0() {
offsetTop = c * radius;
offsetBottom = c * radius;
offsetLeft = c * radius;
offsetRight = c * radius;
}
private Ball mStatusPoint1;
/**
* 動畫狀態1 (0~0.2)
*/
private void animStatus1() {
float percent = mAnimPercent * 5f;
if (mDirection == DIRECTION_LEFT) {
leftX = mStartPoint.leftX - percent * mElasticDistance;
} else if (mDirection == DIRECTION_RIGHT) {
rightX = mStartPoint.rightX + percent * mElasticDistance;
} else if (mDirection == DIRECTION_UP) {
topY = mStartPoint.topY - percent * mElasticDistance;
} else if (mDirection == DIRECTION_DOWN) {
bottomY = mStartPoint.bottomY + percent * mElasticDistance;
}
mStatusPoint1.refresh(x, y, topX, topY, bottomX, bottomY,
leftX, leftY, rightX, rightY);
}
private Ball mStatusPoint2;
/**
* 動畫狀態2 (0.2~0.5)
*/
private void animStatus2() {
float percent = (float) ((mAnimPercent - 0.2) * (10f / 3));
if (mDirection == DIRECTION_LEFT) {
leftX = mStatusPoint1.leftX - percent * (mMoveDistance / 2 - mElasticDistance / 2 );
x = mStatusPoint1.x - percent * (mMoveDistance / 2);
rightX = mStatusPoint1.rightX - percent * (mMoveDistance / 2 - mElasticDistance / 2 );
topX = x;
bottomX = x;
//偏移值稍作變化
offsetTop = radius * c + radius * ( c2 - c ) * percent;
offsetBottom = radius * c + radius * ( c2 - c ) * percent;
} else if (mDirection == DIRECTION_RIGHT) {
rightX = mStatusPoint1.rightX + percent * (mMoveDistance / 2 - mElasticDistance / 2 );
x = mStatusPoint1.x + percent * (mMoveDistance / 2);
leftX = mStatusPoint1.leftX + percent * (mMoveDistance / 2 - mElasticDistance / 2 );
topX = x;
bottomX = x;
//偏移值稍作變化
offsetTop = radius * c + radius * ( c2 - c ) * percent;
offsetBottom = radius * c + radius * ( c2 - c ) * percent;
} else if (mDirection == DIRECTION_UP) {
topY = mStatusPoint1.topY - percent * (mMoveDistance / 2 - mElasticDistance / 2 );
y = mStatusPoint1.y - percent * (mMoveDistance / 2);
bottomY = mStatusPoint1.bottomY - percent * (mMoveDistance / 2 - mElasticDistance / 2 );
leftY = y;
rightY = y;
//偏移值稍作變化
offsetLeft = radius * c + radius * ( c2 - c ) * percent;
offsetRight = radius * c + radius * ( c2 - c ) * percent;
} else if (mDirection == DIRECTION_DOWN) {
bottomY = mStatusPoint1.bottomY + percent * (mMoveDistance / 2 - mElasticDistance / 2 );
y = mStatusPoint1.y + percent * (mMoveDistance / 2);
topY = mStatusPoint1.topY + percent * (mMoveDistance / 2 - mElasticDistance / 2 );
leftY = y;
rightY = y;
//偏移值稍作變化
offsetLeft = radius * c + radius * ( c2 - c ) * percent;
offsetRight = radius * c + radius * ( c2 - c ) * percent;
}
mStatusPoint2.refresh(x, y, topX, topY, bottomX, bottomY,
leftX, leftY, rightX, rightY);
}
private Ball mStatusPoint3;
/**
* 動畫狀態3 (0.5~0.8)
*/
private void animStatus3() {
float percent = (mAnimPercent - 0.5f) * (10f / 3f);
if (mDirection == DIRECTION_LEFT) {
leftX = mStatusPoint2.leftX - Math.abs(percent * (mEndPoint.rightX - mStatusPoint2
.rightX));
x = mStatusPoint2.x - Math.abs(percent * (mEndPoint.x - mStatusPoint2.x));
rightX = mStatusPoint2.rightX - Math.abs(percent * (mEndPoint.x - mStatusPoint2.x));
topX = x;
bottomX = x;
//偏移值稍作變化
offsetTop = radius * c2 - radius * ( c2 - c ) * percent;
offsetBottom = radius * c2 - radius * ( c2 - c ) * percent;
} else if (mDirection == DIRECTION_RIGHT) {
rightX = mStatusPoint2.rightX + percent * (mEndPoint.rightX - mStatusPoint2.rightX);
x = mStatusPoint2.x + percent * (mEndPoint.x - mStatusPoint2.x);
leftX = mStatusPoint2.leftX + percent * (mEndPoint.x - mStatusPoint2.x);
topX = x;
bottomX = x;
//偏移值稍作變化
offsetTop = radius * c2 - radius * ( c2 - c ) * percent;
offsetBottom = radius * c2 - radius * ( c2 - c ) * percent;
} else if (mDirection == DIRECTION_UP) {
topY = mStatusPoint2.topY - Math.abs(percent * (mEndPoint.topY - mStatusPoint2
.topY));
y = mStatusPoint2.y - Math.abs(percent * (mEndPoint.y - mStatusPoint2.y));
bottomY = mStatusPoint2.bottomY - Math.abs(percent * (mEndPoint.y - mStatusPoint2.y));
leftY = y;
rightY = y;
//偏移值稍作變化
offsetLeft = radius * c2 - radius * ( c2 - c ) * percent;
offsetRight = radius * c2 - radius * ( c2 - c ) * percent;
} else if (mDirection == DIRECTION_DOWN) {
bottomY = mStatusPoint2.bottomY + percent * (mEndPoint.bottomY - mStatusPoint2
.bottomY);
y = mStatusPoint2.y + percent * (mEndPoint.y - mStatusPoint2.y);
topY = mStatusPoint2.topY + percent * (mEndPoint.y - mStatusPoint2.y);
leftY = y;
rightY = y;
//偏移值稍作變化
offsetLeft = radius * c2 - radius * ( c2 - c ) * percent;
offsetRight = radius * c2 - radius * ( c2 - c ) * percent;
}
mStatusPoint3.refresh(x, y, topX, topY, bottomX, bottomY,
leftX, leftY, rightX, rightY);
}
private Ball mStatusPoint4;
/**
* 動畫狀態4 (0.8~0.9)
*/
private void animStatus4() {
float percent = (float) (mAnimPercent - 0.8) * 10;
if (mDirection == DIRECTION_LEFT) {
rightX = mStatusPoint3.rightX - percent * (Math.abs(mEndPoint.rightX - mStatusPoint3
.rightX) + mElasticDistance/2);
//再做一次賦值,防止和終點不重合
leftX = mEndPoint.leftX;
x = mEndPoint.x;
bottomX = mEndPoint.bottomX;
topX = mEndPoint.topX;
} else if (mDirection == DIRECTION_RIGHT) {
leftX = mStatusPoint3.leftX + percent * (mEndPoint.leftX - mStatusPoint3.leftX +
mElasticDistance/2);
//再做一次賦值,防止和終點不重合
rightX = mEndPoint.rightX;
x = mEndPoint.x;
bottomX = mEndPoint.bottomX;
topX = mEndPoint.topX;
} else if (mDirection == DIRECTION_UP) {
bottomY = mStatusPoint3.bottomY - percent * (Math.abs(mEndPoint.bottomY - mStatusPoint3
.bottomY) + mElasticDistance/2);
//再做一次賦值,防止和終點不重合
topY = mEndPoint.topY;
y = mEndPoint.y;
leftY = mEndPoint.leftY;
rightY = mEndPoint.rightY;
} else if (mDirection == DIRECTION_DOWN) {
topY = mStatusPoint3.topY + percent * (mEndPoint.topY - mStatusPoint3
.topY + mElasticDistance/2);
//再做一次賦值,防止和終點不重合
bottomY = mEndPoint.bottomY;
y = mEndPoint.y;
leftY = mEndPoint.leftY;
rightY = mEndPoint.rightY;
}
mStatusPoint4.refresh(x, y, topX, topY, bottomX, bottomY,
leftX, leftY, rightX, rightY);
}
private Ball mStatusPoint5;
/**
* 動畫狀態5 (0.9~1)回彈
*/
private void animStatus5() {
float percent = (float) (mAnimPercent - 0.9) * 10;
if (mDirection == DIRECTION_LEFT) {
rightX = mStatusPoint4.rightX + percent * (mEndPoint.rightX - mStatusPoint4.rightX);
} else if (mDirection == DIRECTION_RIGHT) {
leftX = mStatusPoint4.leftX + percent * (mEndPoint.leftX - mStatusPoint4.leftX);
} else if (mDirection == DIRECTION_UP) {
bottomY = mStatusPoint4.bottomY + percent * (mEndPoint.bottomY - mStatusPoint4.bottomY);
} else if (mDirection == DIRECTION_DOWN) {
topY = mStatusPoint4.topY + percent * (mEndPoint.topY - mStatusPoint4.topY);
}
mStatusPoint5.refresh(x, y, topX, topY, bottomX, bottomY,
leftX, leftY, rightX, rightY);
}
/**
* 繪制彈性圓
* 通過繪制四段三階貝塞爾曲線,來實現有彈性變化的圓
* @param topX
* @param topY
* @param offsetTop1
* @param offsetTop2
* @param bottomX
* @param bottomY
* @param offsetBottom1
* @param offsetBottom2
* @param leftX
* @param leftY
* @param offsetLeft1
* @param offsetLeft2
* @param rightX
* @param rightY
* @param offsetRight1
* @param offsetRight2
* @return
*/
private Path drawElasticCircle(
float topX, float topY, float offsetTop1, float offsetTop2,
float bottomX, float bottomY, float offsetBottom1, float offsetBottom2,
float leftX, float leftY, float offsetLeft1, float offsetLeft2,
float rightX, float rightY, float offsetRight1, float offsetRight2
) {
/**
* 繪制每一段三階貝塞爾曲線需要兩個控制點
*/
PointF controlTop1, controlTop2, controlBottom1, controlBottom2,
controlLeft1, controlLeft2, controlRight1, controlRight2;
controlTop1 = new PointF();
controlTop1.x = topX - offsetTop1;
controlTop1.y = topY;
controlTop2 = new PointF();
controlTop2.x = topX + offsetTop2;
controlTop2.y = topY;
controlBottom1 = new PointF();
controlBottom1.x = bottomX - offsetBottom1;
controlBottom1.y = bottomY;
controlBottom2 = new PointF();
controlBottom2.x = bottomX + offsetBottom2;
controlBottom2.y = bottomY;
controlLeft1 = new PointF();
controlLeft1.x = leftX;
controlLeft1.y = leftY - offsetLeft1;
controlLeft2 = new PointF();
controlLeft2.x = leftX;
controlLeft2.y = leftY + offsetLeft2;
controlRight1 = new PointF();
controlRight1.x = rightX;
controlRight1.y = rightY - offsetRight1;
controlRight2 = new PointF();
controlRight2.x = rightX;
controlRight2.y = rightY + offsetRight2;
Path path = new Path();
/**
* 繪制top到left的圓弧
*/
path.moveTo(topX, topY);
path.cubicTo(controlTop1.x, controlTop1.y, controlLeft1.x, controlLeft1.y, leftX, leftY);
/**
* 繪制left到bottom的圓弧
*/
path.cubicTo(controlLeft2.x ,controlLeft2.y, controlBottom1.x, controlBottom1.y, bottomX,
bottomY);
/**
* 繪制bottom到right的圓弧
*/
path.cubicTo(controlBottom2.x, controlBottom2.y, controlRight2.x, controlRight2.y,
rightX, rightY);
/**
* 繪制right到top的圓弧
*/
path.cubicTo(controlRight1.x, controlRight1.y, controlTop2.x, controlTop2.y, topX, topY);
return path;
}
/**
* 求兩點之間的距離
* @param x1 第一個點的橫坐標
* @param y1 第一個點的縱坐標
* @param x2 第二個點的橫坐標
* @param y2 第二個點的縱坐標
* @return 兩點距離
*/
private float getDistance(float x1, float y1, float x2, float y2) {
return (float) Math.sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2));
}
}

貝塞爾曲線還有很多應用的地方,或者說在各個領域都有。
去年開始在黃同學的影響下,慢慢地去實現一些利用貝塞爾曲線實現的效果,源碼有相當一部分代碼也是來自於黃同學,也得益於網絡上大多數技術博客無私的分享,希望自己能夠通過學習這樣一個開發的繪圖曲線,有所提高。
 【源碼分析】Android系統啟動流程
【源碼分析】Android系統啟動流程
Android的啟動過程是從init開始的,它是所有後續進程的祖進程。系統啟動的過程可以大致分為以下幾個步驟1,init.c的啟動 掛載目錄 初始化 解析配置文件2
 Android 自定義View 密碼框實例代碼
Android 自定義View 密碼框實例代碼
暴露您view中所有影響可見外觀的屬性或者行為。•通過XML添加和設置樣式•通過元素的屬性來控制其外觀和行為,支持和重要事件交流的事件監聽器詳細步
 android編程實現懸浮窗體的方法
android編程實現懸浮窗體的方法
本文實例講述了android編程實現懸浮窗體的方法。分享給大家供大家參考,具體如下:突然對懸浮窗體感興趣,查資料做了個小Demo,效果是點擊按鈕後,關閉當前Activit
 華為EMUI 5.0新系統怎麼樣 EMUI 5.0新系統什麼時候發布
華為EMUI 5.0新系統怎麼樣 EMUI 5.0新系統什麼時候發布
華為手機基於Android打造了EMUI系統,目前最新版本是EMUI 4.1,版本是Android 6.0。據荷蘭媒體報道,他們從產業鏈獲悉,華為正在秘研E