ACdream 1210 Chinese Girls' Amusement (規律+數學)
【題意】:
求最大的k<=n/2使得gcd(n,k)=1。
如果n是2m+1形式的,那麼k=m就是答案;
如果n是4m形式的,那麼k=2m-1就是答案;
如果n是4m+2形式的,那麼k=2m-1就是答案。
證明略,需要簡單的高精度。
java代碼:
//感覺就是暴力 從n/2 開始減 ,直到互素為止,
import java.io.*;
import java.util.*;
import java.math.BigInteger;//聲明BigInteger大數類
import java.lang.*;
public class Main
{
public static void main(String args[])
{
Scanner cin = new Scanner(System.in);
BigInteger n,k;
n=cin.nextBigInteger();
k=n.divide(new BigInteger(2));
while(n.gcd(k).compareTo(BigInteger.ONE)!=0)
{
k=k.subtract(BigInteger.ONE);
}
System.out.println(k);
}
}
ACdream 1211 Reactor Cooling【上下界網絡流 + 輸出流量】
題意:
給n個點,及m根pipe,每根pipe用來流躺液體的,單向的,每時每刻每根pipe流進來的物質要等於流出去的物質,要使得m條pipe組成一個循環體,裡面流躺物質。
並且滿足每根pipe一定的流量限制,范圍為[Li,Ri].即要滿足每時刻流進來的不能超過Ri(最大流問題),同時最小不能低於Li。
例如:
46(4個點,6個pipe)
12 1 3 (1->2上界為3,下界為1)
23 1 3
3 4 1 3
4 1 1 3
1 3 1 3
4 2 1 3
可行流:
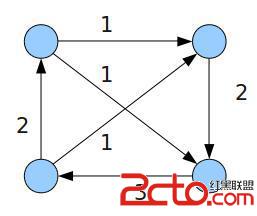
再如:所有pipe的上界為2下界為1的話,就不能得到一種可行流。
題解:
上界用ci表示,下界用bi表示。
下界是必須流滿的,那麼對於每一條邊,去掉下界後,其自由流為ci– bi。
主要思想:每一個點流進來的流=流出去的流
對於每一個點i,令
Mi= sum(i點所有流進來的下界流)– sum(i點所有流出去的下界流)
如果Mi大於0,代表此點必須還要流出去Mi的自由流,那麼我們從源點連一條Mi的邊到該點。
如果Mi小於0,代表此點必須還要流進來Mi的自由流,那麼我們從該點連一條Mi的邊到匯點。
如果求S->T的最大流,看是否滿流(S的相鄰邊都流滿)。
滿流則有解,否則無解。
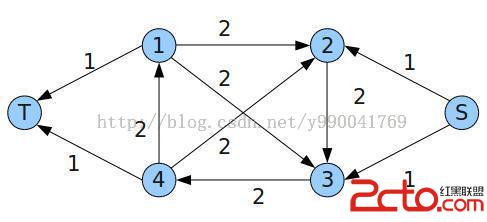
代碼:
/*
*上下界的網絡流,用上界減去下界
* Problem: ACdream 1211
* Running time: 16MS
* Complier: G++
* Author: herongwei
* Create Time: 19:59 2015/10/8 星期四
*/
#include
#include
#include
#include
#include


 Android NDK學習筆記3-入門案例篇
Android NDK學習筆記3-入門案例篇
 Android IPC機制(四):細說Binder連接池
Android IPC機制(四):細說Binder連接池
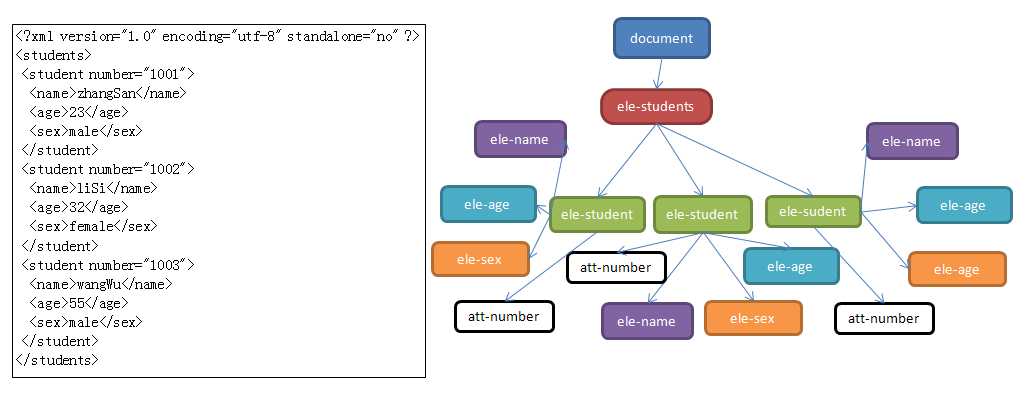 XML解析器
XML解析器
 解析網絡json數據並展示到ListView上
解析網絡json數據並展示到ListView上