本文主要講解局部加權(線性)回歸。在講解局部加權線性回歸之前，先講解兩個概念：欠擬合、過擬合，由此引出局部加權線性回歸算法。

欠擬合、過擬合

如下圖中三個擬合模型。第一個是一個線性模型，對訓練數據擬合不夠好，損失函數取值較大。如圖中第二個模型，如果我們在線性模型上加一個新特征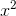項，擬合結果就會好一些。圖中第三個是一個包含5階多項式的模型，對訓練數據幾乎完美擬合。

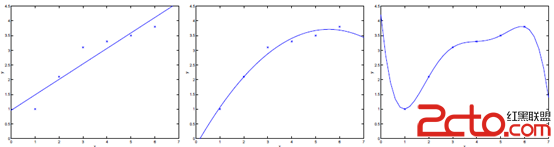
模型一沒有很好的擬合訓練數據，在訓練數據以及在測試數據上都存在較大誤差，這種情況稱之為欠擬合（underfitting）。

模型三對訓練數據擬合的很不錯，但是在測試數據上的准確度並不理想。這種對訓練數據擬合較好，而在測試數據上准確度較低的情況稱之為過擬合（overfitting）。

局部加權線性回歸（Locally weighted linear regression，LWR）

從上面欠擬合和過擬合的例子中我們可以體會到，在回歸預測模型中，預測模型的准確度特別依賴於特征的選擇。特征選擇不合適，往往會導致預測結果的天壤之別。局部加權線性回歸很好的解決了這個問題，它的預測性能不太依賴於選擇的特征，又能很好的避免欠擬合和過擬合的風險。

在理解局部加權線性回歸前，先回憶一下線性回歸。線性回歸的損失函數把訓練數據中的樣本看做是平等的，並沒有權重的概念。線性回歸的詳細請參考《線性回歸、梯度下降》，它的主要思想為：

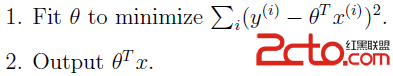
而局部加權線性回歸，在構造損失函數時加入了權重w，對距離預測點較近的訓練樣本給以較高的權重，距離預測點較遠的訓練樣本給以較小的權重。權重的取值范圍是(0,1)。

局部加權線性回歸的主要思想是：

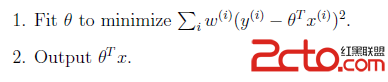
其中假設權重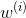符合公式

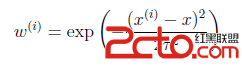
公式中權重大小取決於預測點x與訓練樣本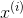的距離。如果|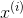- x|較小，那麼取值接近於1，反之接近0。參數τ稱為bandwidth，用於控制權重的變化幅度。

局部加權線性回歸優點是不太依賴特征選擇，而且只需要用線性模型就訓練出不錯的擬合模型。

但是由於局部加權線性回歸是一個非參數學習算法，損失數隨著預測值的不同而不同，這樣θ無法事先確定，每次預測時都需要掃描所有數據重新計算θ，所以計算量比較大。