編輯:關於Android編程
之前實現過html5版的鐘表,html5也有一個畫板屬性Canvas,相對於安卓的Canvas來說html5的功能要強大的多,就拿鐘表的實現,html5要方便簡單的多,而安卓實現起來則非常復雜,像指針轉動,html5可以畫一條線,然後可以用這條線旋轉一個弧度即可,而安卓必須是已知起點坐標和終點坐標,這就需要精確計算起始坐標了。先看下效果圖,因為是圖靜態的,動態圖也懶得做,所以看個大致效果即可,具體效果可以下載demo觀看:

這個鐘表並不算完美,正常的鐘表,秒針每轉動一格,分針和時針都會跟著轉動相應的弧度,但本例中偷了個懶,只有秒針轉一周時,分針才移動一小格,分針轉一周時,時針移動一大格,不滿一周的情況下不動,因為畫線需要精確的坐標值,如果做到這種效果那工作量可就大了去了,因此我們知道原理即可。
實現思路:
1.重寫View,並在ondraw方法中繪圖;
2.定義邊框寬度,刻度寬度,長度,指針寬度,長度,計算圓心坐標及表盤半徑;
3.繪制邊框:
mPaint.setStrokeWidth(bordWidth); // 設置圓環的寬度
mPaint.setColor(bordColor);
canvas.drawCircle(getWidth()/2, getWidth()/2, r, mPaint);
//畫刻度
//12
mPaint.setStrokeWidth(timeLineB_W);
mPaint.setColor(timeColor);
canvas.drawLine(circleX,bordWidth, circleX, bordWidth+timeLineB_H, mPaint);
//12-1
mPaint.setStrokeWidth(timeLineS_W);
for(int i=1;i<6;i++){
canvas.drawLine((float)(circleX+r*Math.cos(Math.toRadians(90-i*6)) ),(float)(circleX-r*Math.cos(Math.toRadians(i*6))), (float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(90-i*6))),(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(i*6))),mPaint);
}
//1
mPaint.setStrokeWidth(timeLineB_W);
canvas.drawLine((float)(circleX+r*Math.cos(Math.toRadians(60)) ),(float)(circleX-r*Math.cos(Math.toRadians(30))), (float)(circleX+(r-timeLineB_H)*Math.cos(Math.toRadians(60))),(float)(circleX-(r-timeLineB_H)*Math.cos(Math.toRadians(30))),mPaint);
//1-2
mPaint.setStrokeWidth(timeLineS_W);
for(int i=1;i<6;i++){
canvas.drawLine((float)(circleX+r*Math.cos(Math.toRadians(90-30-i*6)) ),(float)(circleX-r*Math.cos(Math.toRadians(30+i*6))), (float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(90-30-i*6))),(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(30+i*6))),mPaint);
}
//2
mPaint.setStrokeWidth(timeLineB_W);
canvas.drawLine((float)(circleX+r*Math.cos(Math.toRadians(30)) ),(float)(circleX-r*Math.cos(Math.toRadians(60))), (float)(circleX+(r-timeLineB_H)*Math.cos(Math.toRadians(30))),(float)(circleX-(r-timeLineB_H)*Math.cos(Math.toRadians(60))),mPaint);
//2-3
mPaint.setStrokeWidth(timeLineS_W);
for(int i=1;i<6;i++){
canvas.drawLine((float)(circleX+r*Math.cos(Math.toRadians(90-60-i*6)) ),(float)(circleX-r*Math.cos(Math.toRadians(60+i*6))), (float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(90-60-i*6))),(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(60+i*6))),mPaint);
}
//3
mPaint.setStrokeWidth(timeLineB_W);
canvas.drawLine(getWidth()-bordWidth, circleX, getWidth()-bordWidth-timeLineB_H, circleX, mPaint);
//3-4
mPaint.setStrokeWidth(timeLineS_W);
for(int i=1;i<6;i++){
canvas.drawLine((float)(circleX+r*Math.cos(Math.toRadians(i*6)) ),(float)(circleX+r*Math.cos(Math.toRadians(90-i*6))), (float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(i*6))),(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(90-i*6))),mPaint);
}
//4
mPaint.setStrokeWidth(timeLineB_W);
canvas.drawLine((float)(circleX+r*Math.cos(Math.toRadians(30)) ),(float)(circleX+r*Math.cos(Math.toRadians(60))), (float)(circleX+(r-timeLineB_H)*Math.cos(Math.toRadians(30))),(float)(circleX+(r-timeLineB_H)*Math.cos(Math.toRadians(60))),mPaint);
//4-5
mPaint.setStrokeWidth(timeLineS_W);
for(int i=1;i<6;i++){
canvas.drawLine((float)(circleX+r*Math.cos(Math.toRadians(30+i*6)) ),(float)(circleX+r*Math.cos(Math.toRadians(90-30-i*6))), (float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(30+i*6))),(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(90-30-i*6))),mPaint);
}
//5
mPaint.setStrokeWidth(timeLineB_W);
canvas.drawLine((float)(circleX+r*Math.cos(Math.toRadians(60)) ),(float)(circleX+r*Math.cos(Math.toRadians(30))), (float)(circleX+(r-timeLineB_H)*Math.cos(Math.toRadians(60))),(float)(circleX+(r-timeLineB_H)*Math.cos(Math.toRadians(30))),mPaint);
//5-6
mPaint.setStrokeWidth(timeLineS_W);
for(int i=1;i<6;i++){
canvas.drawLine((float)(circleX+r*Math.cos(Math.toRadians(60+i*6)) ),(float)(circleX+r*Math.cos(Math.toRadians(90-60-i*6))), (float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(60+i*6))),(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(90-60-i*6))),mPaint);
}
//6
mPaint.setStrokeWidth(timeLineB_W);
canvas.drawLine(circleX,getWidth()-bordWidth, circleX, getWidth()-bordWidth-timeLineB_H,mPaint);
//6-7
mPaint.setStrokeWidth(timeLineS_W);
for(int i=1;i<6;i++){
canvas.drawLine((float)(circleX-r*Math.cos(Math.toRadians(90-i*6)) ),(float)(circleX+r*Math.cos(Math.toRadians(i*6))), (float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(90-i*6))),(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(i*6))),mPaint);
}
//7
mPaint.setStrokeWidth(timeLineB_W);
canvas.drawLine((float)(circleX-r*Math.cos(Math.toRadians(60)) ),(float)(circleX+r*Math.cos(Math.toRadians(30))), (float)(circleX-(r-timeLineB_H)*Math.cos(Math.toRadians(60))),(float)(circleX+(r-timeLineB_H)*Math.cos(Math.toRadians(30))),mPaint);
//7-8
mPaint.setStrokeWidth(timeLineS_W);
for(int i=1;i<6;i++){
canvas.drawLine((float)(circleX-r*Math.cos(Math.toRadians(90-30-i*6)) ),(float)(circleX+r*Math.cos(Math.toRadians(30+i*6))), (float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(90-30-i*6))),(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(30+i*6))),mPaint);
}
//8
mPaint.setStrokeWidth(timeLineB_W);
canvas.drawLine((float)(circleX-r*Math.cos(Math.toRadians(30)) ),(float)(circleX+r*Math.cos(Math.toRadians(60))), (float)(circleX-(r-timeLineB_H)*Math.cos(Math.toRadians(30))),(float)(circleX+(r-timeLineB_H)*Math.cos(Math.toRadians(60))),mPaint);
//8-9
mPaint.setStrokeWidth(timeLineS_W);
for(int i=1;i<6;i++){
canvas.drawLine((float)(circleX-r*Math.cos(Math.toRadians(90-60-i*6)) ),(float)(circleX+r*Math.cos(Math.toRadians(60+i*6))), (float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(90-60-i*6))),(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(60+i*6))),mPaint);
}
//9
mPaint.setStrokeWidth(timeLineB_W);
canvas.drawLine(bordWidth,circleX, bordWidth+timeLineB_H, circleX,mPaint);
//9-10
mPaint.setStrokeWidth(timeLineS_W);
for(int i=1;i<6;i++){
canvas.drawLine((float)(circleX-r*Math.cos(Math.toRadians(i*6)) ),(float)(circleX-r*Math.cos(Math.toRadians(90-i*6))), (float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(i*6))),(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(90-i*6))),mPaint);
}
//10
mPaint.setStrokeWidth(timeLineB_W);
canvas.drawLine((float)(circleX-r*Math.cos(Math.toRadians(30)) ),(float)(circleX-r*Math.cos(Math.toRadians(60))), (float)(circleX-(r-timeLineB_H)*Math.cos(Math.toRadians(30))),(float)(circleX-(r-timeLineB_H)*Math.cos(Math.toRadians(60))),mPaint);
//10-11
mPaint.setStrokeWidth(timeLineS_W);
for(int i=1;i<6;i++){
canvas.drawLine((float)(circleX-r*Math.cos(Math.toRadians(30+i*6)) ),(float)(circleX-r*Math.cos(Math.toRadians(90-30-i*6))), (float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(30+i*6))),(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(90-30-i*6))),mPaint);
}
//11
mPaint.setStrokeWidth(timeLineB_W);
canvas.drawLine((float)(circleX-r*Math.cos(Math.toRadians(60)) ),(float)(circleX-r*Math.cos(Math.toRadians(30))), (float)(circleX-(r-timeLineB_H)*Math.cos(Math.toRadians(60))),(float)(circleX-(r-timeLineB_H)*Math.cos(Math.toRadians(30))),mPaint);
//11-12
mPaint.setStrokeWidth(timeLineS_W);
for(int i=1;i<6;i++){
canvas.drawLine((float)(circleX-r*Math.cos(Math.toRadians(60+i*6)) ),(float)(circleX-r*Math.cos(Math.toRadians(90-60-i*6))), (float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(60+i*6))),(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(90-60-i*6))),mPaint);
}
刻度是逐一計算起始點坐標並繪制的,拿1點的刻度來說,
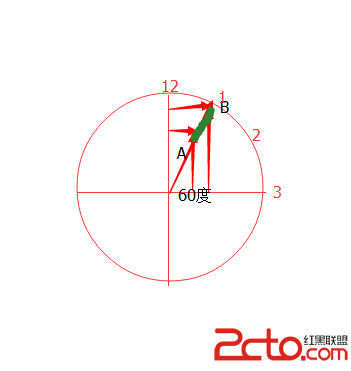
已知圓心坐標(x,y),半徑r,AB長度為a,求A點B點坐標。這應該是初中的題目了吧,很好計算,只要求出A點到y軸和x軸的距離,B點到y軸和x軸的距離即可(最方便的辦法就是利用正余玄函數了,而Java也提供了正余玄函數的算法:Math.cos(Math.toRadians(角度值),因為Math.cos傳的是弧度,所以要將角度轉化為弧度如Math.toRadians(60)),當然要注意屏幕坐標與數學中的象限坐標是不同的,所以AB點坐標要用求出的距離值結合圓的半徑求出該點在屏幕中的實際坐標,然後畫線即可。
5.繪制指針交點:
mPaint.setStrokeWidth(2); mPaint.setStyle(Paint.Style.FILL); canvas.drawCircle(circleX,circleX, 10, mPaint);6.秒針轉動:
到這裡,我們得思考下,鐘表是要動的啊,那怎麼實現打開應用鐘表就開始走呢?很簡單吧,初始化View時,在View的構造方法中開啟個線程去不斷重繪View即可,時間間隔當然為一秒,這也就給你視覺感是指針一秒轉動一次,另外需要你對秒針分針時針轉動時相互關聯所走的角度有一個清晰的思路,如果你連他們之間的關系都搞不明白,那看代碼就更不用說了:
while (true){
if (ss == 360){
mm++;//秒針每轉一圈,分針走一格,一格6度,一圈60格
if(mm==60){
hh++;//分針轉一圈,時針走一格,一格30度,一圈12格
if(hh==12){
hh=0;
}
mm=0;
}
ss = 0;
}
postInvalidate(); //重繪
try{
Thread.sleep(1000); //暫停1秒
} catch (InterruptedException e){
e.printStackTrace();
}
ss+=6; //360度,分針每秒轉動6度
}
mPaint.setStrokeWidth(timeLineS_W-5);//設置秒針寬度
mPaint.setColor(pointColor);
r=r-timeLineB_H-5;//設置秒針長度
//分針隨秒針轉動
if(ss<=30){
canvas.drawLine(circleX,circleX,(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(90-ss*1))),(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(ss*1))), mPaint);
}else if(ss<=60){
canvas.drawLine(circleX,circleX,(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(90-30-(ss-30)*1))),(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(30+(ss-30)*1))), mPaint);
}else if(ss<=90){
canvas.drawLine(circleX,circleX,(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(90-60-(ss-60)*1))),(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(60+(ss-60)*1))), mPaint);
}else if(ss<=120){
canvas.drawLine(circleX,circleX,(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians((ss-90)*1))),(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(90-(ss-90)*1))), mPaint);
}else if(ss<=150){
canvas.drawLine(circleX,circleX,(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(30+(ss-120)*1))),(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(90-30-(ss-120)*1))), mPaint);
}else if(ss<=180){
canvas.drawLine(circleX,circleX,(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(60+(ss-150)*1))),(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(90-60-(ss-150)*1))), mPaint);
}else if(ss<=210){
canvas.drawLine(circleX,circleX,(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(90-(ss-180)*1))),(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians((ss-180)*1))), mPaint);
}else if(ss<=240){
canvas.drawLine(circleX,circleX,(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(90-30-(ss-210)*1))),(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(30+(ss-210)*1))), mPaint);
}else if(ss<=270){
canvas.drawLine(circleX,circleX,(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(90-60-(ss-240)*1))),(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(60+(ss-240)*1))), mPaint);
}else if(ss<=300){
canvas.drawLine(circleX,circleX,(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians((ss-270)*1))),(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(90-(ss-270)*1))),mPaint);
}else if(ss<=330){
canvas.drawLine(circleX,circleX,(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(30+(ss-300)*1))),(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(90-30-(ss-300)*1))),mPaint);
}else if(ss<=360){
canvas.drawLine(circleX,circleX,(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(60+(ss-330)*1))),(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(90-60-(ss-330)*1))),mPaint);
}
mPaint.setStrokeWidth(timeLineS_W);//設置分針寬度
r=circleX-bordWidth;//還原
r=r-timeLineB_H-50;//設置分針長度
//分針隨秒針轉動
if(mm<=5){
canvas.drawLine(circleX,circleX,(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(90-mm*6))),(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(mm*6))), mPaint);
}else if(mm<=10){
canvas.drawLine(circleX,circleX,(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(90-30-(mm-5)*6))),(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(30+(mm-5)*6))), mPaint);
}else if(mm<=15){
canvas.drawLine(circleX,circleX,(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(90-60-(mm-10)*6))),(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(60+(mm-10)*6))), mPaint);
}else if(mm<=20){
canvas.drawLine(circleX,circleX,(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians((mm-15)*6))),(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(90-(mm-15)*6))), mPaint);
}else if(mm<=25){
canvas.drawLine(circleX,circleX,(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(30+(mm-20)*6))),(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(90-30-(mm-20)*6))), mPaint);
}else if(mm<=30){
canvas.drawLine(circleX,circleX,(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(60+(mm-25)*6))),(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(90-60-(mm-25)*6))), mPaint);
}else if(mm<=35){
canvas.drawLine(circleX,circleX,(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(90-(mm-30)*6))),(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians((mm-30)*6))), mPaint);
}else if(mm<=40){
canvas.drawLine(circleX,circleX,(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(90-30-(mm-35)*6))),(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(30+(mm-35)*6))), mPaint);
}else if(mm<=45){
canvas.drawLine(circleX,circleX,(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(90-60-(mm-40)*6))),(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(60+(mm-40)*6))), mPaint);
}else if(mm<=50){
canvas.drawLine(circleX,circleX,(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians((mm-45)*6))),(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(90-(mm-45)*6))),mPaint);
}else if(mm<=55){
canvas.drawLine(circleX,circleX,(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(30+(mm-50)*6))),(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(90-30-(mm-50)*6))),mPaint);
}else if(mm<=60){
canvas.drawLine(circleX,circleX,(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(60+(mm-55)*6))),(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(90-30-(mm-55)*6))),mPaint);
}
r=circleX-bordWidth;//還原
r=r-timeLineB_H-120;//設置時針長度
//時針隨分針轉動
if(hh<=3){
canvas.drawLine(circleX,circleX,(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(90-hh*30))),(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(hh*30))), mPaint);
}else if(hh<=6){
canvas.drawLine(circleX,circleX,(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians((hh-3)*30))),(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians(90-(hh-3)*30))), mPaint);
}else if(hh<=9){
canvas.drawLine(circleX,circleX,(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(90-(hh-6)*30))),(float)(circleX+(r-timeLineS_H)*Math.cos(Math.toRadians((hh-6)*30))), mPaint);
}else if(hh<=12){
canvas.drawLine(circleX,circleX,(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians((hh-9)*30))),(float)(circleX-(r-timeLineS_H)*Math.cos(Math.toRadians(90-(hh-9)*30))),mPaint);
}
//寫時刻數字 mPaint.setTextSize(26); mPaint.setStrokeWidth(2); mPaint.setColor(bordColor); canvas.drawText(12, circleX-timeLineB_W, bordWidth+timeLineB_H+30, mPaint); canvas.drawText(1, (float)(circleX+(r-timeLineB_H)*Math.cos(Math.toRadians(60)))-20,(float)(circleX-(r-timeLineB_H)*Math.cos(Math.toRadians(30)))+20, mPaint); canvas.drawText(2, (float)(circleX+(r-timeLineB_H)*Math.cos(Math.toRadians(30)))-20,(float)(circleX-(r-timeLineB_H)*Math.cos(Math.toRadians(60)))+20, mPaint); canvas.drawText(3, getWidth()-bordWidth-timeLineB_H-20, circleX+10, mPaint); canvas.drawText(4,(float)(circleX+(r-timeLineB_H)*Math.cos(Math.toRadians(30)))-20,(float)(circleX+(r-timeLineB_H)*Math.cos(Math.toRadians(60))), mPaint); canvas.drawText(5, (float)(circleX+(r-timeLineB_H)*Math.cos(Math.toRadians(60)))-15,(float)(circleX+(r-timeLineB_H)*Math.cos(Math.toRadians(30)))-5, mPaint); canvas.drawText(6,circleX-10, getWidth()-bordWidth-timeLineB_H-10, mPaint); canvas.drawText(7, (float)(circleX-(r-timeLineB_H)*Math.cos(Math.toRadians(60))),(float)(circleX+(r-timeLineB_H)*Math.cos(Math.toRadians(30)))-10, mPaint); canvas.drawText(8, (float)(circleX-(r-timeLineB_H)*Math.cos(Math.toRadians(30)))+10,(float)(circleX+(r-timeLineB_H)*Math.cos(Math.toRadians(60)))+5, mPaint); canvas.drawText(9, bordWidth+timeLineB_H+10, circleX+10, mPaint); canvas.drawText(10, (float)(circleX-(r-timeLineB_H)*Math.cos(Math.toRadians(30)))+10,(float)(circleX-(r-timeLineB_H)*Math.cos(Math.toRadians(60)))+20, mPaint); canvas.drawText(11, (float)(circleX-(r-timeLineB_H)*Math.cos(Math.toRadians(60))),(float)(circleX-(r-timeLineB_H)*Math.cos(Math.toRadians(30)))+25, mPaint);
 Android之——應用更新功能
Android之——應用更新功能
一、概述相信大家都遇到過這種情況,就是在Android手機中的應用,往往在應用的設置裡面,都會有一個檢查更新的功能,如果應用開發商或者運營商發布了新的應用版本,點擊設置裡
 Android 仿百度手機助手首頁滑動效果
Android 仿百度手機助手首頁滑動效果
今天看到百度手機助手首頁上的滑動效果非常nice,主要功能歸結為: 1、當手指上劃時,頂部搜索欄隨手指移動距離而縮小到隱藏,隱藏後內容還是可以繼續移動 2、手指下滑時,當
 Android ExpandableListView的使用
Android ExpandableListView的使用
ExpandableListView可擴展列表一般可用來開發類似QQ聯系人的界面效果。簡單整理了一下ExpandableListView的使用,希望幫助到需要的親們,由於
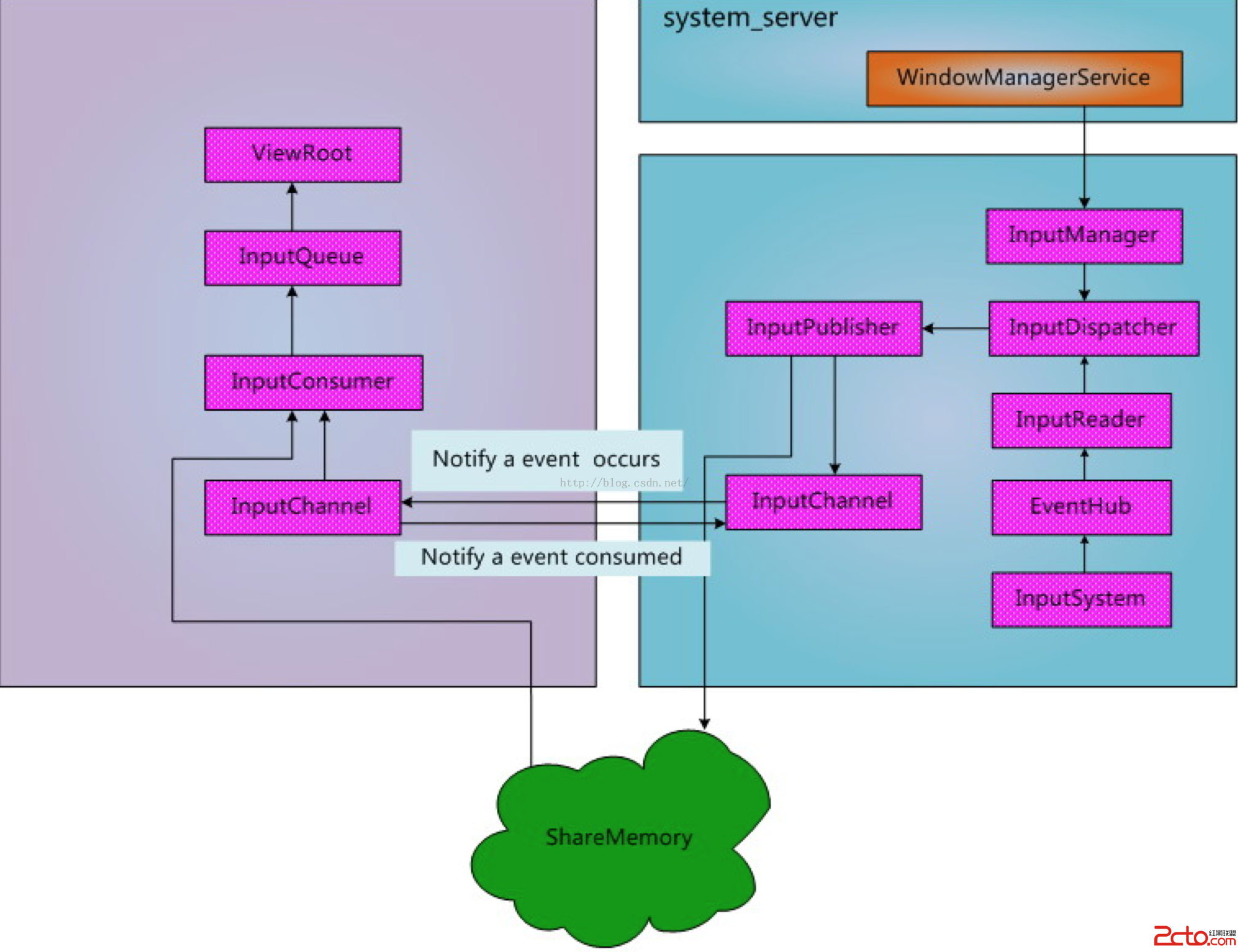 Android Touch事件傳遞機制全面解析(從WMS到View樹)
Android Touch事件傳遞機制全面解析(從WMS到View樹)
轉眼間近一年沒更新博客了,工作一忙起來,很難有時間來寫博客了,由於現在也在從事Android開發相關的工作,因此以後的博文也會更多地專注於這一塊。這篇文章准備從源碼層面為