編輯：關於Android編程
OpenCV 2.4.9的SVM程序是基於LibSVMv2.6。LibSVM是由台灣大學林智仁等開發的用於SVM分類和回歸的開源機器學習工具包。
在進行源碼分析之前，我們先給出用於SVM算法的訓練參數結構變量CvSVMParams：
struct CvSVMParams
{
CvSVMParams();
CvSVMParams( int _svm_type, int _kernel_type,
double _degree, double _gamma, double _coef0,
double _C, double _nu, double _p,
CvMat* _class_weights, CvTermCriteria _term_crit );
int svm_type;
int kernel_type;
double degree; // for poly
double gamma; // for poly/rbf/sigmoid
double coef0; // for poly/sigmoid
double C; // for CV_SVM_C_SVC, CV_SVM_EPS_SVR and CV_SVM_NU_SVR
double nu; // for CV_SVM_NU_SVC, CV_SVM_ONE_CLASS, and CV_SVM_NU_SVR
double p; // for CV_SVM_EPS_SVR
CvMat* class_weights; // for CV_SVM_C_SVC
CvTermCriteria term_crit; // termination criteria
};
svm_type表示OpenCV能夠實現的SVM的類型：C-SVC、ν-SVC、單類SVM、ε-SVR和ν-SVR，對應的變量分別為：CvSVM::C_SVC、CvSVM::NU_SVC、CvSVM::ONE_CLASS、CvSVM::EPS_SVR和CvSVM::NU_SVR
kernel_type表示OpenCV能夠實現的核函數的類型：線性核函數、多項式核函數、高斯核函數和Sigmoid核函數，對應的變量分別為：CvSVM::LINEAR、CvSVM::POLY、CvSVM::RBF和CvSVM::SIGMOID
degree表示多項式核函數（式54）中的參數q
gamma表示多項式核函數（式54）、高斯核函數（式56）和Sigmoid核函數（式57）中的參數γ
coef0表示多項式核函數（式54）和Sigmoid核函數（式57）中的參數p
C表示懲罰參數C
nu表示ν-SVC和ν-SVR的參數ν
p表示ε-SVR的參數ε
class_weights表示不同分類的權值，該值與參數C相乘後，實現了不同分類的不同懲罰力度，該值越大，該類別的誤分類數據的懲罰就越大
term_crit:SVM表示廣義SMO算法的迭代過程的終止條件，該變量是結構數據類型：
typedef struct CvTermCriteria
{
//CV_TERMCRIT_ITER（表示使用迭代次數作為終止條件）和CV_TERMCRIT_EPS（表示使用精度作為終止條件）二值之一，或者二者的組合
int type;
int max_iter; //最大迭代次數
double epsilon; //結果的精確性
}
下面是類CvSVM的缺省構造函數：
CvSVM::CvSVM()
{
decision_func = 0; //表示決策函數，數據類型為CvSVMDecisionFunc
class_labels = 0; //表示分類問題的類標簽
class_weights = 0; //表示分類問題的類別權重
storage = 0; //表示存儲空間
var_idx = 0; //表示用到的特征屬性的索引
kernel = 0; //表示核函數，數據類型為CvSVMKernel
solver = 0; //表示廣義SMO算法的求解，數據類型為類CvSVMSolver
default_model_name = "my_svm";
clear(); //清空一些全局變量
}
下面是SVM的訓練函數：
bool CvSVM::train( const CvMat* _train_data, const CvMat* _responses,
const CvMat* _var_idx, const CvMat* _sample_idx, CvSVMParams _params )
//_train_data表示訓練樣本數據集
//_responses表示訓練樣本的響應值
//_var_idx表示真正用到的特征屬性的索引
//_sample_idx表示真正用到的訓練樣本的索引
//_params表示SVM算法所需要的一些參數，如SVM的類型，核函數的類型等
{
bool ok = false; //用於該函數的正確返回標識
CvMat* responses = 0; //表示樣本的響應值
CvMemStorage* temp_storage = 0; //暫存
const float** samples = 0; //表示完整的訓練樣本數據
CV_FUNCNAME( "CvSVM::train" );
__BEGIN__;
//svm_type表示SVM類型，sample_count表示訓練樣本的數量，var_count表示特征屬性的數量，sample_size表示訓練樣本的存儲空間的尺寸大小
int svm_type, sample_count, var_count, sample_size;
int block_size = 1 << 16; //先定義一個很大的存儲空間的尺寸大小
//表示拉格朗日乘子α，但我們在實際計算中，已經把5種SVM轉換為統一的f(β)形式，因此這裡的alpha表示的是式150、式151、式152、式154和式156中β，在後面的程序中，涉及到拉格朗日乘子α的，本質上指的都是β
double* alpha;
clear(); //清空一些全局變量
//調用set_params函數，為全局變量params賦值（它的數據類型為CvSVMParams，用於表示SVM算法所需的一些參數），並判斷params中元素的正確性
CV_CALL( set_params( _params ));
svm_type = _params.svm_type; //表示SVM的類型
/* Prepare training data and related parameters */
//調用cvPrepareTrainData函數，為SVM算法准備樣本數據，即初始化樣本。首先檢查樣本_train_data，該變量矩陣一定要是CV_ROW_SAMPLE，即矩陣的行表示樣本，列表示特征屬性；然後賦值樣本響應值，如果SVM類型為CvSVM::ONE_CLASS，響應值為0，否則為_responses，並且如果SVM為CvSVM::C_SVC或CvSVM::NU_SVC，響應值_responses的類型為CV_VAR_CATEGORICAL，即為分類，否則為CV_VAR_ORDERED，即為回歸；再根據_sample_idx和_var_idx確定那些真正要用到的樣本數據以及那些真正要用到的特征屬性；最終得到完整的樣本數據samples。
CV_CALL( cvPrepareTrainData( "CvSVM::train", _train_data, CV_ROW_SAMPLE,
svm_type != CvSVM::ONE_CLASS ? _responses : 0,
svm_type == CvSVM::C_SVC ||
svm_type == CvSVM::NU_SVC ? CV_VAR_CATEGORICAL :
CV_VAR_ORDERED, _var_idx, _sample_idx,
false, &samples, &sample_count, &var_count, &var_all,
&responses, &class_labels, &var_idx ));
//得到訓練樣本的存儲空間大小
sample_size = var_count*sizeof(samples[0][0]);
// make the storage block size large enough to fit all
// the temporary vectors and output support vectors.
//定義一個足夠大的存儲空間，用於滿足所有的暫存向量和輸出支持向量
block_size = MAX( block_size, sample_count*(int)sizeof(CvSVMKernelRow));
block_size = MAX( block_size, sample_count*2*(int)sizeof(double) + 1024 );
block_size = MAX( block_size, sample_size*2 + 1024 );
//下面三條語句雖然略有不同，但基本上實現的功能都是分配內存空間並初始化
CV_CALL( storage = cvCreateMemStorage(block_size + sizeof(CvMemBlock) + sizeof(CvSeqBlock)));
CV_CALL( temp_storage = cvCreateChildMemStorage(storage));
CV_CALL( alpha = (double*)cvMemStorageAlloc(temp_storage, sample_count*sizeof(double)));
// create_kernel函數的作用是通過參數params得到參數kernel，即得到核函數
create_kernel();
// create_solver函數的作用是實例化CvSVMSolver類，得到參數solver
create_solver();
//調用do_train函數，真正完成SVM訓練任務，後面給出了該函數的詳細講解
if( !do_train( svm_type, sample_count, var_count, samples, responses, temp_storage, alpha ))
EXIT;
//表示成功得到了SVM模型
ok = true; // model has been trained succesfully
__END__;
//釋放一些不再使用的變量和內存空間
delete solver;
solver = 0;
cvReleaseMemStorage( &temp_storage );
cvReleaseMat( &responses );
cvFree( &samples );
if( cvGetErrStatus() < 0 || !ok )
clear();
return ok; //返回
}
do_train函數的詳細講解：
bool CvSVM::do_train( int svm_type, int sample_count, int var_count, const float** samples,
const CvMat* responses, CvMemStorage* temp_storage, double* alpha )
// svm_type表示SVM算法的類型
// sample_count表示訓練樣本的數量
// var_count表示特征屬性的數量
// samples表示完整的訓練樣本數據
// responses表示訓練樣本的響應值
// temp_storage表示訓練所需的內存空間
// alpha表示拉格朗日乘子α，實際為式148中的變量β
{
bool ok = false; //用於該函數的正確返回標識
CV_FUNCNAME( "CvSVM::do_train" );
__BEGIN__;
CvSVMDecisionFunc* df = 0; //表示SVM的決策函數
const int sample_size = var_count*sizeof(samples[0][0]); //定義樣本空間大小
int i, j, k;
cvClearMemStorage( storage ); //清空storage內存空間
if( svm_type == ONE_CLASS || svm_type == EPS_SVR || svm_type == NU_SVR )
//如果SVM的類型為單類SVM、ε-SVR或ν-SVR
{
int sv_count = 0; //表示支持向量的數量
//為變量df（決策函數）分配內存空間，並把它的首地址指針指向變量decision_func
CV_CALL( decision_func = df =
(CvSVMDecisionFunc*)cvAlloc( sizeof(df[0]) ));
df->rho = 0; //初始化決策函數中的變量ρ，ρ實質為偏移量b
//調用train1函數，該函數作用主要是根據SVM類型的不同，參數solver實現不同的SMO算法函數：類型為C_SVC，實現的是solver->solve_c_svc函數；類型為NU_SVC，實現的是solver->solve_nu_svc函數；類型為ONE_CLASS，實現的是solver->solve_one_class函數；類型為EPS_SVR，實現的是solver->solve_eps_svr函數；類型為NU_SVR，實現的是solver->solve_nu_svr函數。這5個函數在後面都會給出詳細的講解
//在這裡SVM的類型只能為ONE_CLASS、EPS_SVR或NU_SVR
if( !train1( sample_count, var_count, samples, svm_type == ONE_CLASS ? 0 :
responses->data.i, 0, 0, temp_storage, alpha, df->rho ))
EXIT;
//遍歷所有訓練樣本，統計支持向量的數量，只有αi大於0的向量才是支持向量
for( i = 0; i < sample_count; i++ )
sv_count += fabs(alpha[i]) > 0;
CV_Assert(sv_count != 0); //確保不能沒有支持向量
sv_total = df->sv_count = sv_count; //賦值支持向量的數量
//為支持向量數據sv和拉格朗日乘子df->alpha開辟一塊存儲空間
CV_CALL( df->alpha = (double*)cvMemStorageAlloc( storage, sv_count*sizeof(df->alpha[0])) );
CV_CALL( sv = (float**)cvMemStorageAlloc( storage, sv_count*sizeof(sv[0])));
//遍歷訓練樣本
for( i = k = 0; i < sample_count; i++ )
{
if( fabs(alpha[i]) > 0 ) //拉格朗日乘子αi大於0
{
//得到支持向量的樣本數據sv，以及它所對應的αi值df->alpha
CV_CALL( sv[k] = (float*)cvMemStorageAlloc( storage, sample_size ));
memcpy( sv[k], samples[i], sample_size );
df->alpha[k++] = alpha[i];
}
}
}
else //SVM類型為C-SVC和ν-SVC，即分類問題
{
int class_count = class_labels->cols; //得到樣本的類別數量
int* sv_tab = 0; //用於標識某一樣本是否為支持向量
const float** temp_samples = 0; //表示暫時需要使用的訓練樣本
// class_ranges表示分類范圍，例如有9個樣本，共三類，並且已經按照響應值的大小進行了排序，結果為：1,1,1,2,2,3,3,3,3，則class_ranges[0]=0, class_ranges[1]=3, class_ranges[2]=5, class_ranges[3]=9，因此通過該變量很容易得到每類的樣本數，以及它們的分布范圍
int* class_ranges = 0;
schar* temp_y = 0; //表示暫時需要使用的訓練樣本的分類標簽
//再次確認是分類問題
assert( svm_type == CvSVM::C_SVC || svm_type == CvSVM::NU_SVC );
//如果是C_SVC類型，並且初始化了變量params.class_weights
if( svm_type == CvSVM::C_SVC && params.class_weights )
{
const CvMat* cw = params.class_weights; //為類別權重賦值
//判斷類別權重cw的數據格式是否正確，即cw必須是一維的矩陣形式，即向量，向量的元素數量必須等於分類數量，並且數據類型必須為CV_32FC1或CV_64FC1
if( !CV_IS_MAT(cw) || (cw->cols != 1 && cw->rows != 1) ||
cw->rows + cw->cols - 1 != class_count ||
(CV_MAT_TYPE(cw->type) != CV_32FC1 && CV_MAT_TYPE(cw->type) != CV_64FC1) )
CV_ERROR( CV_StsBadArg, "params.class_weights must be 1d floating-point vector "
"containing as many elements as the number of classes" );
//把cw賦值給全局變量class_weights
CV_CALL( class_weights = cvCreateMat( cw->rows, cw->cols, CV_64F ));
CV_CALL( cvConvert( cw, class_weights ));
//實現了該等式：class_weights = class_weights × params.C
CV_CALL( cvScale( class_weights, class_weights, params.C ));
}
//為變量df（決策函數）分配內存空間，並把它的首地址指針指向變量decision_func
CV_CALL( decision_func = df = (CvSVMDecisionFunc*)cvAlloc(
(class_count*(class_count-1)/2)*sizeof(df[0])));
//分配內存空間給sv_tab，並清零
CV_CALL( sv_tab = (int*)cvMemStorageAlloc( temp_storage, sample_count*sizeof(sv_tab[0]) ));
memset( sv_tab, 0, sample_count*sizeof(sv_tab[0]) );
//分配內存空間給class_ranges，temp_samples和temp_y
CV_CALL( class_ranges = (int*)cvMemStorageAlloc( temp_storage,
(class_count + 1)*sizeof(class_ranges[0])));
CV_CALL( temp_samples = (const float**)cvMemStorageAlloc( temp_storage,
sample_count*sizeof(temp_samples[0])));
CV_CALL( temp_y = (schar*)cvMemStorageAlloc( temp_storage, sample_count));
class_ranges[class_count] = 0; //清零
//調用cvSortSamplesByClasses函數，實現了按照響應值對樣本進行升序排序，並得到了變量class_ranges
cvSortSamplesByClasses( samples, responses, class_ranges, 0 );
//check that while cross-validation there were the samples from all the classes
//確保class_ranges[class_count]必須大於0，交叉驗證時要用到
if( class_ranges[class_count] <= 0 )
CV_ERROR( CV_StsBadArg, "While cross-validation one or more of the classes have "
"been fell out of the sample. Try to enlarge " );
if( svm_type == NU_SVC ) //如果為NU_SVC類型
{
// check if nu is feasible
//得到樣本中任意兩個類別的樣本數，檢查ν-SVC中的參數ν是否滿足式66的條件
for(i = 0; i < class_count; i++ ) //遍歷樣本的所有類別
{
int ci = class_ranges[i+1] - class_ranges[i]; //得到第i個類別的樣本數量
for( j = i+1; j< class_count; j++ ) //遍歷當前類別以後的所有類別
{
//得到第j個類別的樣本數量，第j個類別在第i個類別的排序後面
int cj = class_ranges[j+1] - class_ranges[j];
//如果不滿足式66的條件，則退出程序
if( params.nu*(ci + cj)*0.5 > MIN( ci, cj ) )
{
// !!!TODO!!! add some diagnostic
EXIT; // exit immediately; will release the model and return NULL pointer
}
}
}
}
// train n*(n-1)/2 classifiers
//下面的for循環實現了一對一的多類SVC方法
//得到n*(n-1)/2個SVM分類器，這裡的n表示分類數，即class_count，每一個SVM分類器的信息都單獨存儲在自己的df變量中
for( i = 0; i < class_count; i++ ) //遍歷所有類別
{
for( j = i+1; j < class_count; j++, df++ ) //遍歷當前分類以後的所有類別
{
//si和sj分別表示第i個類別和第j個類別在排序後樣本的起始索引值
//ci和cj分別表示第i個類別和第j個類別的樣本數量
int si = class_ranges[i], ci = class_ranges[i+1] - si;
int sj = class_ranges[j], cj = class_ranges[j+1] - sj;
//Cn和Cp分別表示負例和正例的懲罰參數
double Cp = params.C, Cn = Cp;
//k1用於計數索引，sv_count表示支持向量的數量
int k1 = 0, sv_count = 0;
for( k = 0; k < ci; k++ ) //遍歷第i個類別的所有樣本
{
temp_samples[k] = samples[si + k]; //第i個類別的所有樣本
temp_y[k] = 1; //第i個類別的樣本分類標簽，設為1
}
for( k = 0; k < cj; k++ ) //遍歷第j個類別的所有樣本
{
temp_samples[ci + k] = samples[sj + k]; //第j個類別的所有樣本
temp_y[ci + k] = -1; //第j個類別的樣本分類標簽，設為-1
}
if( class_weights ) //如果應用分類權重class_weights這個參數
{
//Cp和Cn分別為加權後的第i個和第j個類別的懲罰參數
Cp = class_weights->data.db[i];
Cn = class_weights->data.db[j];
}
//調用train1函數，該函數作用主要是根據SVM類型的不同，參數solver實現不同的SMO算法函數：類型為C_SVC，實現的是solver->solve_c_svc函數；類型為NU_SVC，實現的是solver->solve_nu_svc函數；類型為ONE_CLASS，實現的是solver->solve_one_class函數；類型為EPS_SVR，實現的是solver->solve_eps_svr函數；類型為NU_SVR，實現的是solver->solve_nu_svr函數。這5個函數在後面都會給出詳細的講解
//在這裡SVM的類型只能為C_SVC或NU_SVC
if( !train1( ci + cj, var_count, temp_samples, temp_y,
Cp, Cn, temp_storage, alpha, df->rho ))
EXIT;
//遍歷第i個和第j個類別的所有樣本，得到當前分類器的支持向量數量
for( k = 0; k < ci + cj; k++ )
sv_count += fabs(alpha[k]) > 0;
df->sv_count = sv_count; //賦值當前分類器的支持向量數量
//為拉格朗日乘子df->alpha和支持向量索引df->sv_index開辟一塊存儲空間
CV_CALL( df->alpha = (double*)cvMemStorageAlloc( temp_storage,
sv_count*sizeof(df->alpha[0])));
CV_CALL( df->sv_index = (int*)cvMemStorageAlloc( temp_storage,
sv_count*sizeof(df->sv_index[0])));
for( k = 0; k < ci; k++ ) //遍歷第i個類別的樣本
{
if( fabs(alpha[k]) > 0 ) //拉格朗日乘子αi大於0
{
sv_tab[si + k] = 1; //標注該樣本為支持向量
//當前分類器的支持向量在樣本序列的索引值
df->sv_index[k1] = si + k;
df->alpha[k1++] = alpha[k]; //賦值當前分類器的支持向量αi
}
}
for( k = 0; k < cj; k++ ) //遍歷第j個類別的樣本
{
if( fabs(alpha[ci + k]) > 0 ) //拉格朗日乘子αi大於0
{
sv_tab[sj + k] = 1; //標注該樣本為支持向量
//當前分類器的支持向量在樣本序列的索引值
df->sv_index[k1] = sj + k;
df->alpha[k1++] = alpha[ci + k]; //賦值當前分類器的支持向量αi
}
}
}
} //訓練n*(n-1)/2個SVM分類器結束
// allocate support vectors and initialize sv_tab
for( i = 0, k = 0; i < sample_count; i++ ) //遍歷所有訓練樣本
{
//在前面計算n*(n-1)/2個SVM分類器的過程中，無論對於哪一個分類器，只要某一樣本為支持向量，它的sv_tab都為1，在這裡sv_tab又被賦值為全部樣本下支持向量的計數值，即當前支持向量是全部支持向量的第幾個支持向量
if( sv_tab[i] )
sv_tab[i] = ++k;
}
sv_total = k; //得到了支持向量的數量
//為支持向量數據sv分配存儲空間
CV_CALL( sv = (float**)cvMemStorageAlloc( storage, sv_total*sizeof(sv[0])));
for( i = 0, k = 0; i < sample_count; i++ ) //遍歷所有樣本
{
if( sv_tab[i] ) //如果當前樣本是支持向量
{
//得到支持向量的樣本數據sv
CV_CALL( sv[k] = (float*)cvMemStorageAlloc( storage, sample_size ));
memcpy( sv[k], samples[i], sample_size );
k++; //計數值累加
}
}
df = (CvSVMDecisionFunc*)decision_func; //決策函數的指針重新定位
// set sv pointers
//重新設置df->sv_index，以前變量df->sv_index[i]表示的是當前分類器的第i個支持向量在當前訓練樣本序列的索引值，而現在經過下面多重for循環，df->sv_index[i]表示的是當前分類器的第i個支持向量在全部訓練樣本中所有支持向量的第幾個支持向量減1
//再次遍歷n*(n-1)/2個SVM分類器
for( i = 0; i < class_count; i++ ) //遍歷所有分類
{
for( j = i+1; j < class_count; j++, df++ ) //遍歷當前分類以後的所有分類
{
//遍歷當前SVM分類器的所有支持向量
for( k = 0; k < df->sv_count; k++ )
{
//為df->sv_index重新賦值
df->sv_index[k] = sv_tab[df->sv_index[k]]-1;
//確保df->sv_index的值必須小於所有支持向量的總數
assert( (unsigned)df->sv_index[k] < (unsigned)sv_total );
}
}
}
}
//對於使用線性核函數的SVM來說，即式53，它們的支持向量是呈現線性的，因此只需用一個支持向量就可以代表所有的支持向量，這麼可以簡化SVM模型，optimize_linear_svm函數就實現了這個功能，該函數的詳見講解見後面
optimize_linear_svm();
ok = true; //返回變量賦值
__END__;
return ok; //函數返回
}
用於求解C-SVC類型的廣義SMO算法：
bool CvSVMSolver::solve_c_svc( int _sample_count, int _var_count, const float** _samples, schar* _y,
double _Cp, double _Cn, CvMemStorage* _storage,
CvSVMKernel* _kernel, double* _alpha, CvSVMSolutionInfo& _si )
{
int i;
//調用create函數，用於設置廣義SMO算法的參數，在後面給出該函數的詳細講解
//對於C-SVC，select_working_set_func函數指針指向select_working_set，calc_rho_func函數指針指向calc_rho，get_row_func函數指針指向get_row_svc，_Cp和_Cn分別表示正例和負例的懲罰參數C
if( !create( _sample_count, _var_count, _samples, _y, _sample_count,
_alpha, _Cp, _Cn, _storage, _kernel, &CvSVMSolver::get_row_svc,
&CvSVMSolver::select_working_set, &CvSVMSolver::calc_rho ))
return false;
//遍歷所有樣本，清空alpha數組，賦值b數組
for( i = 0; i < sample_count; i++ )
{
alpha[i] = 0; //α即為式148中的β，對於C-SVC，β初始化為0
b[i] = -1; //b即為式148中的p，對於C-SVC（式150），p為-1
}
//調用solve_generic，執行廣義SMO算法的迭代過程，該函數在後面給出詳細的講解
if( !solve_generic( _si ))
return false;
//遍歷所有樣本，使負例的β為負值，當再次用到alpha[i]時，會取絕對值，因此正負無所謂，這麼做的好處是可以通過alpha[i]值，就能看出是正例還是負例
for( i = 0; i < sample_count; i++ )
alpha[i] *= y[i];
return true;
}
用於求解ν-SVC類型的廣義SMO算法：
bool CvSVMSolver::solve_nu_svc( int _sample_count, int _var_count, const float** _samples, schar* _y,
CvMemStorage* _storage, CvSVMKernel* _kernel,
double* _alpha, CvSVMSolutionInfo& _si )
{
int i;
double sum_pos, sum_neg, inv_r;
//調用create函數，用於設置廣義SMO算法的參數，在後面給出該函數的詳細講解
//對於ν-SVC，select_working_set_func函數指針指向select_working_set_nu_svm，calc_rho_func函數指針指向calc_rho_nu_svm，get_row_func函數指針指向get_row_svc
if( !create( _sample_count, _var_count, _samples, _y, _sample_count,
_alpha, 1., 1., _storage, _kernel, &CvSVMSolver::get_row_svc,
&CvSVMSolver::select_working_set_nu_svm, &CvSVMSolver::calc_rho_nu_svm ))
return false;
// sum_pos = sum_neg =νN/2，用於初始化β，詳見原理部分的解釋
sum_pos = kernel->params->nu * sample_count * 0.5;
sum_neg = kernel->params->nu * sample_count * 0.5;
//遍歷所有樣本
for( i = 0; i < sample_count; i++ )
{
if( y[i] > 0 ) //正例下，β的初始化
{
alpha[i] = MIN(1.0, sum_pos);
sum_pos -= alpha[i];
}
else //負例下，β的初始化
{
alpha[i] = MIN(1.0, sum_neg);
sum_neg -= alpha[i];
}
b[i] = 0; //b即為式148中的p，對於ν-SVC（式151），p為0
}
//調用solve_generic，執行廣義SMO算法的迭代過程，該函數在後面給出詳細的講解
if( !solve_generic( _si ))
return false;
//_si.r為原理部分式142下面段落中的ρ*，則inv_r就為1/ρ*
inv_r = 1./_si.r;
//遍歷所有拉格朗日乘子，得到α＝α*/ρ*
for( i = 0; i < sample_count; i++ )
alpha[i] *= y[i]*inv_r;
_si.rho *= inv_r; //得到b＝b*/ρ*
_si.obj *= (inv_r*inv_r); //目標函數也要除以ρ*的平方
_si.upper_bound_p = inv_r; //賦值正界
_si.upper_bound_n = inv_r; //賦值負界
return true;
}
用於求解單類SVM類型的廣義SMO算法：
bool CvSVMSolver::solve_one_class( int _sample_count, int _var_count, const float** _samples,
CvMemStorage* _storage, CvSVMKernel* _kernel,
double* _alpha, CvSVMSolutionInfo& _si )
{
int i, n;
double nu = _kernel->params->nu; //得到參數ν
//調用create函數，用於設置廣義SMO算法的參數，在後面給出該函數的詳細講解
//對於單類SVM，select_working_set_func函數指針指向select_working_set，calc_rho_func函數指針指向calc_rho，get_row_func函數指針指向get_row_one_class
if( !create( _sample_count, _var_count, _samples, 0, _sample_count,
_alpha, 1., 1., _storage, _kernel, &CvSVMSolver::get_row_one_class,
&CvSVMSolver::select_working_set, &CvSVMSolver::calc_rho ))
return false;
//為變量y分配空間
y = (schar*)cvMemStorageAlloc( storage, sample_count*sizeof(y[0]) );
n = cvRound( nu*sample_count ); //定義n=[vN]
//遍歷所有樣本
for( i = 0; i < sample_count; i++ )
{
y[i] = 1; //單類SVM的所有樣本的響應值都設為1
b[i] = 0; //b即為式148中的p，對於ν-SVC（式152），p為0
alpha[i] = i < n ? 1 : 0; //初始化β，詳見原理部分的解釋
}
//初始化因四捨五入而產生的小數部分對應的β
if( n < sample_count )
alpha[n] = nu * sample_count - n;
else
alpha[n-1] = nu * sample_count - (n-1);
//調用solve_generic，執行廣義SMO算法的迭代過程，該函數在後面給出詳細的講解
return solve_generic(_si);
}
用於求解ε-SVR類型的廣義SMO算法：
bool CvSVMSolver::solve_eps_svr( int _sample_count, int _var_count, const float** _samples,
const float* _y, CvMemStorage* _storage,
CvSVMKernel* _kernel, double* _alpha, CvSVMSolutionInfo& _si )
{
int i;
//p表示ε-SVR類型的參數ε，kernel_param_c表示懲罰參數C
double p = _kernel->params->p, kernel_param_c = _kernel->params->C;
//調用create函數，用於設置廣義SMO算法的參數，在後面給出該函數的詳細講解
//對於ε-SVR，select_working_set_func函數指針指向select_working_set，calc_rho_func函數指針指向calc_rho，get_row_func函數指針指向get_row_svr
if( !create( _sample_count, _var_count, _samples, 0,
_sample_count*2, 0, kernel_param_c, kernel_param_c, _storage, _kernel, &CvSVMSolver::get_row_svr,
&CvSVMSolver::select_working_set, &CvSVMSolver::calc_rho ))
return false;
//為y和alpha開辟內存空間，它們的長度都為樣本數量N的2倍
y = (schar*)cvMemStorageAlloc( storage, sample_count*2*sizeof(y[0]) );
alpha = (double*)cvMemStorageAlloc( storage, alpha_count*sizeof(alpha[0]) );
//遍歷所有樣本，初始化參數
for( i = 0; i < sample_count; i++ )
{
//前N個參數
alpha[i] = 0; //β初始化為0，前N個β即為α―
//b即為式148中的p，對於ε-SVR（式154），前N個p為εeT－yT
b[i] = p - _y[i];
//y對應於式154中的z，對於ε-SVR（式154），前N個z為1
y[i] = 1;
//後N個參數
alpha[i+sample_count] = 0; //β初始化為0，後N個β即為α＋
//b即為式148中的p，對於ε-SVR（式154），後N個p為εeT+yT
b[i+sample_count] = p + _y[i];
//y對應於式154中的z，對於ε-SVR（式154），後N個z為-1
y[i+sample_count] = -1;
}
//調用solve_generic，執行廣義SMO算法的迭代過程，該函數在後面給出詳細的講解
if( !solve_generic( _si ))
return false;
//遍歷所有樣本，計算ε-SVR的決策函數（式105）中核函數前的系數α――α＋
for( i = 0; i < sample_count; i++ )
_alpha[i] = alpha[i] - alpha[i+sample_count];
return true;
}
用於求解ν-SVR類型的廣義SMO算法：
bool CvSVMSolver::solve_nu_svr( int _sample_count, int _var_count, const float** _samples,
const float* _y, CvMemStorage* _storage,
CvSVMKernel* _kernel, double* _alpha, CvSVMSolutionInfo& _si )
{
int i;
// kernel_param_c表示懲罰參數C
double kernel_param_c = _kernel->params->C, sum;
//調用create函數，用於設置廣義SMO算法的參數，在後面給出該函數的詳細講解
//對於ν-SVR，select_working_set_func函數指針指向select_working_set_nu_svm，calc_rho_func函數指針指向calc_rho_nu_svm，get_row_func函數指針指向get_row_svr
if( !create( _sample_count, _var_count, _samples, 0,
_sample_count*2, 0, 1., 1., _storage, _kernel, &CvSVMSolver::get_row_svr,
&CvSVMSolver::select_working_set_nu_svm, &CvSVMSolver::calc_rho_nu_svm ))
return false;
//為y和alpha開辟內存空間，它們的長度都為樣本數量N的2倍
y = (schar*)cvMemStorageAlloc( storage, sample_count*2*sizeof(y[0]) );
alpha = (double*)cvMemStorageAlloc( storage, alpha_count*sizeof(alpha[0]) );
//sum = CνN/2
sum = kernel_param_c * _kernel->params->nu * sample_count * 0.5;
//遍歷所有樣本，初始化參數
for( i = 0; i < sample_count; i++ )
{
//初始化β，詳見原理部分的解釋
alpha[i] = alpha[i + sample_count] = MIN(sum, kernel_param_c);
sum -= alpha[i];
//b即為式148中的p，對於ν-SVR（式156），前N個p為－yT
b[i] = -_y[i];
//y對應於式156中的z，對於ν-SVR（式156），前N個z為1
y[i] = 1;
//b即為式148中的p，對於ν-SVR（式156），後N個p為yT
b[i + sample_count] = _y[i];
//y對應於式156中的z，對於ν-SVR（式156），後N個z為-1
y[i + sample_count] = -1;
}
//調用solve_generic，執行廣義SMO算法的迭代過程，該函數在後面給出詳細的講解
if( !solve_generic( _si ))
return false;
//遍歷所有樣本，計算ν-SVR的決策函數（式116）中核函數前的系數α――α＋
for( i = 0; i < sample_count; i++ )
_alpha[i] = alpha[i] - alpha[i+sample_count];
return true;
}
create函數主要用於初始化和設置廣義SMO算法的一些參數：
bool CvSVMSolver::create( int _sample_count, int _var_count, const float** _samples, schar* _y,
int _alpha_count, double* _alpha, double _Cp, double _Cn,
CvMemStorage* _storage, CvSVMKernel* _kernel, GetRow _get_row,
SelectWorkingSet _select_working_set, CalcRho _calc_rho )
//_sample_count表示訓練樣本的數量
//_var_count表示特征屬性的數量
//_samples表示訓練樣本的數據集
//_y表示樣本的響應值
//_alpha_count表示拉格朗日乘子αi的數量
//_alpha表示拉格朗日乘子αi的值
//_Cp表示對於SVC的正例的懲罰參數
//_Cn表示對於SVC的負例的懲罰參數
//_storage表示一塊存儲空間
//_kernel表示核函數
//_get_row表示得到矩陣Q的列的首地址
//_select_working_set表示選取工作集βi和βj
//_calc_rho表示計算ρ
{
bool ok = false; //該函數返回的標識變量
int i, svm_type; //svm_type表示SVM類型
CV_FUNCNAME( "CvSVMSolver::create" );
__BEGIN__;
int rows_hdr_size; //矩陣Q的列的首地址指針尺寸大小
clear(); //清空一些全局變量
sample_count = _sample_count; //訓練樣本的數量
var_count = _var_count; //特征屬性的數量
samples = _samples; //訓練樣本
y = _y; //樣本響應值
alpha_count = _alpha_count; //拉格朗日乘子αi的數量
alpha = _alpha; //拉格朗日乘子αi的值
kernel = _kernel; //核函數
C[0] = _Cn; //負例的懲罰參數
C[1] = _Cp; //正例的懲罰參數
eps = kernel->params->term_crit.epsilon; //表示式170和式171中的ε
max_iter = kernel->params->term_crit.max_iter; //表示最大迭代次數
storage = cvCreateChildMemStorage( _storage ); //開辟內存空間
//為變量b，alpha_status，G和buf開辟內存空間
//b表示式148中的參數p；alpha_status表示拉格朗日乘子αi（實質是βi）的狀態，即βi是下界（βi=0），上界（βi=C），還是其他；G表示式149；buf在函數get_row調用時會用到
b = (double*)cvMemStorageAlloc( storage, alpha_count*sizeof(b[0]));
alpha_status = (schar*)cvMemStorageAlloc( storage, alpha_count*sizeof(alpha_status[0]));
G = (double*)cvMemStorageAlloc( storage, alpha_count*sizeof(G[0]));
for( i = 0; i < 2; i++ )
buf[i] = (Qfloat*)cvMemStorageAlloc( storage, sample_count*2*sizeof(buf[i][0]) );
svm_type = kernel->params->svm_type; //SVM類型
//函數指針賦值，該函數的作用是選擇工作集βi和βj
select_working_set_func = _select_working_set;
//如果函數指針select_working_set_func沒有被賦值，則根據SVM的類型來確定該函數
if( !select_working_set_func )
//如果是ν-SVC或ν-SVR，select_working_set_func = select_working_set_nu_svm；如果是C-SVC、單類SVM或ε-SVR，select_working_set_func= select_working_set
select_working_set_func = svm_type == CvSVM::NU_SVC || svm_type == CvSVM::NU_SVR ?
&CvSVMSolver::select_working_set_nu_svm : &CvSVMSolver::select_working_set;
//函數指針賦值，作用是計算ρ，即b
calc_rho_func = _calc_rho;
//如果函數指針calc_rho_func沒有被賦值，則根據SVM的類型來確定該函數
if( !calc_rho_func )
//如果是ν-SVC或ν-SVR，calc_rho_func = calc_rho_nu_svm；如果是C-SVC、單類SVM或ε-SVR，calc_rho_func = calc_rho
calc_rho_func = svm_type == CvSVM::NU_SVC || svm_type == CvSVM::NU_SVR ?
&CvSVMSolver::calc_rho_nu_svm : &CvSVMSolver::calc_rho;
//函數指針賦值，作用是得到矩陣Q的列首地址
get_row_func = _get_row;
//如果函數指針get_row_func沒有被賦值，則根據SVM的類型來確定該函數
if( !get_row_func )
//如果是ε-SVR或ν-SVR，get_row_func = get_row_svr；如果是C-SVC或ν-SVC，get_row_func = get_row_svc；如果是單類SVM，get_row_func = get_row_one_class
get_row_func = params->svm_type == CvSVM::EPS_SVR ||
params->svm_type == CvSVM::NU_SVR ? &CvSVMSolver::get_row_svr :
params->svm_type == CvSVM::C_SVC ||
params->svm_type == CvSVM::NU_SVC ? &CvSVMSolver::get_row_svc :
&CvSVMSolver::get_row_one_class;
//定義cache_line_size和cache_size的大小，主要用於get_row_func函數
cache_line_size = sample_count*sizeof(Qfloat);
// cache size = max(num_of_samples^2*sizeof(Qfloat)*0.25, 64Kb)
// (assuming that for large training sets ~25% of Q matrix is used)
cache_size = MAX( cache_line_size*sample_count/4, CV_SVM_MIN_CACHE_SIZE );
// the size of Q matrix row headers
//定義rows_hdr_size大小
rows_hdr_size = sample_count*sizeof(rows[0]);
if( rows_hdr_size > storage->block_size )
CV_ERROR( CV_StsOutOfRange, "Too small storage block size" );
//定義lru_list變量
lru_list.prev = lru_list.next = &lru_list;
rows = (CvSVMKernelRow*)cvMemStorageAlloc( storage, rows_hdr_size );
memset( rows, 0, rows_hdr_size );
ok = true; //設置正確返回變量
__END__;
return ok; //返回
}
廣義SMO算法的迭代過程：
bool CvSVMSolver::solve_generic( CvSVMSolutionInfo& si )
{
int iter = 0; //用於記錄迭代的次數
int i, j, k;
// 1. initialize gradient and alpha status
//遍歷所有拉格朗日乘子αi，得到αi的狀態，程序中的α實質是式148的β
for( i = 0; i < alpha_count; i++ )
{
/****************
#define update_alpha_status(i) \
alpha_status[i] = (schar)(alpha[i] >= get_C(i) ? 1 : alpha[i] <= 0 ? -1 : 0)
****************/
//宏定義update_alpha_status表示得到拉格朗日乘子αi的狀態：當αi等於懲罰參數C時，alpha_status[i]等於1；當αi=0時，alpha_status[i]等於-1；當0<αi 1e200 ) //確保變量G[i]不能過大
return false;
}
for( i = 0; i < alpha_count; i++ ) //遍歷所有拉格朗日乘子αi
{
/*******************
#define is_lower_bound(i) (alpha_status[i] < 0)
#define is_upper_bound(i) (alpha_status[i] > 0)
*******************/
//宏定義is_lower_bound用於表示αi是否為下界，即是否等於0，如果等於0，則is_lower_bound為1，否則為0；宏定義is_upper_bound用於表示αi是否為上界，即是否等於C，如果等於C，則is_upper_bound為1，否則為0
if( !is_lower_bound(i) ) //如果αi≠0
{
//函數get_row表示得到矩陣Q的第i列首地址，Q即為式148中的Q，雖然Qij都可以表示為zizjK(xi, xj)，但不同類型的SVM的zi含義不同，因此在get_row函數內，先通過get_row_base函數得到核函數K(xi, xj)的第i列，然後再調用get_row_func函數，前面已經分析過了，不同的SVM，get_row_func函數的函數指針會指向不同的函數
const Qfloat *Q_i = get_row( i, buf[0] );
double alpha_i = alpha[i]; //得到αi值，實質為βi
//計算式149，得到f(β)的梯度向量▽f(β)，G[j]表示▽f(β)向量的第j個元素
for( j = 0; j < alpha_count; j++ )
G[j] += alpha_i*Q_i[j];
}
}
// 2. optimization loop
for(;;) //優化β的迭代死循環
{
// Q_i和Q_j分別表示式148中的Q的第i列和第j列的首地址
const Qfloat *Q_i, *Q_j;
//C_i和C_j分別表示第i個和第j個樣本所對應的懲罰參數C，如圖10所示
double C_i, C_j;
//old_alpha_i、old_alpha_j、alpha_i和alpha_j分別表示式161中βik、βjk、βinew和βjnew
double old_alpha_i, old_alpha_j, alpha_i, alpha_j;
// delta_alpha_i和delta_alpha_j分別表示每次迭代前後的βi的差值和βj的差值
double delta_alpha_i, delta_alpha_j;
#ifdef _DEBUG
for( i = 0; i < alpha_count; i++ )
{
if( fabs(G[i]) > 1e+300 )
return false;
if( fabs(alpha[i]) > 1e16 )
return false;
}
#endif
//當滿足終止條件或超過最大迭代次數，則退出迭代死循環
// select_working_set_func函數用於工作集βi和βj的選取，如果該函數的返回值為1，則表示終止迭代循環，max_iter表示最大迭代次數。前面已經分析過，不同的SVM，select_working_set_func函數的函數指針會指向不同的函數，第一類SVM指向的是select_working_set函數，第二類SVM指向的是select_working_set_nu_svm，這兩個函數在後面都會給出詳細的講解
if( (this->*select_working_set_func)( i, j ) != 0 || iter++ >= max_iter )
break;
//分別得到矩陣Q的第i列和第j列的首地址
Q_i = get_row( i, buf[0] );
Q_j = get_row( j, buf[1] );
//分別得到第i個和第j個樣本的C值
C_i = get_C(i);
C_j = get_C(j);
//分別得到第i個和第j個樣本的β值
alpha_i = old_alpha_i = alpha[i];
alpha_j = old_alpha_j = alpha[j];
if( y[i] != y[j] ) //zi≠zj時，式160中的第1行
{
double denom = Q_i[i]+Q_j[j]+2*Q_i[j]; //得到式160中第1行的aij
//得到式162中分式的分子部分，即－▽if(β)－▽jf(β)
double delta = (-G[i]-G[j])/MAX(fabs(denom),FLT_EPSILON);
double diff = alpha_i - alpha_j; //得到式164中的T
//得到式162中的βinew和βjnew
alpha_i += delta;
alpha_j += delta;
//如圖10(a)，限制β的值在矩形區域內
if( diff > 0 && alpha_j < 0 ) //區域Ⅲ
{
alpha_j = 0;
alpha_i = diff;
}
else if( diff <= 0 && alpha_i < 0 ) //區域Ⅳ
{
alpha_i = 0;
alpha_j = -diff;
}
if( diff > C_i - C_j && alpha_i > C_i ) //區域Ⅰ
{
alpha_i = C_i;
alpha_j = C_i - diff;
}
else if( diff <= C_i - C_j && alpha_j > C_j ) //區域Ⅱ
{
alpha_j = C_j;
alpha_i = C_j + diff;
}
}
else //zi＝zj時，式160中的第2行
{
double denom = Q_i[i]+Q_j[j]-2*Q_i[j]; //得到式160中第2行的ats
//得到式163中分式的分子部分，即▽if(β)－▽jf(β)
double delta = (G[i]-G[j])/MAX(fabs(denom),FLT_EPSILON);
double sum = alpha_i + alpha_j; //得到式165中的S
//得到式163中的βinew和βjnew
alpha_i -= delta;
alpha_j += delta;
//如圖10(b)，限制β的值在矩形區域內
if( sum > C_i && alpha_i > C_i ) //區域Ⅰ
{
alpha_i = C_i;
alpha_j = sum - C_i;
}
else if( sum <= C_i && alpha_j < 0) //區域Ⅱ
{
alpha_j = 0;
alpha_i = sum;
}
if( sum > C_j && alpha_j > C_j ) //區域Ⅲ
{
alpha_j = C_j;
alpha_i = sum - C_j;
}
else if( sum <= C_j && alpha_i < 0 ) //區域Ⅳ
{
alpha_i = 0;
alpha_j = sum;
}
}
// update alpha
//更新βi和βj，以及它們的狀態
alpha[i] = alpha_i;
alpha[j] = alpha_j;
update_alpha_status(i);
update_alpha_status(j);
// update G
//得到迭代前後βi的差值和βj的差值
delta_alpha_i = alpha_i - old_alpha_i;
delta_alpha_j = alpha_j - old_alpha_j;
//更新▽f(β)
for( k = 0; k < alpha_count; k++ )
G[k] += Q_i[k]*delta_alpha_i + Q_j[k]*delta_alpha_j;
} //迭代優化結束
// calculate rho
// calc_rho_func函數計算ρ，即決策函數中的參數b。前面已經分析過，不同類型的SVM，calc_rho_func函數的函數指針會指向不同的函數，第一類SVM指向的是calc_rho函數，第二類SVM指向的是calc_rho_nu_svm，這兩個函數在後面都會給出詳細的講解
(this->*calc_rho_func)( si.rho, si.r );
// calculate objective value
//計算式148，得到目標函數f(β)的值
//f(β)＝0.5×[βT×(▽f(β)+p)]＝0.5×[βT×(Qβ＋p)+p)]＝0.5×βTQβ＋pTβ
for( i = 0, si.obj = 0; i < alpha_count; i++ )
si.obj += alpha[i] * (G[i] + b[i]);
si.obj *= 0.5;
si.upper_bound_p = C[1]; //正例的懲罰參數C
si.upper_bound_n = C[0]; //負例的懲罰參數C
return true;
}
第一類SVM（C-SVC、單類SVM和ε-SVR）的選取工作集βi和βj的函數：
bool
CvSVMSolver::select_working_set( int& out_i, int& out_j )
//out_i和out_j分別表示βi和βj
{
// return i,j which maximize -grad(f)^T d , under constraint
// if alpha_i == C, d != +1
// if alpha_i == 0, d != -1
//定義一個最大值
double Gmax1 = -DBL_MAX; // max { -grad(f)_i * d | y_i*d = +1 }
int Gmax1_idx = -1; //初始化i=-1
//定義一個最大值
double Gmax2 = -DBL_MAX; // max { -grad(f)_i * d | y_i*d = -1 }
int Gmax2_idx = -1; //初始化j＝－1
int i;
//遍歷所有β
for( i = 0; i < alpha_count; i++ )
{
double t;
if( y[i] > 0 ) // y = +1，即式166中的zt＝1
{
if( !is_upper_bound(i) && (t = -G[i]) > Gmax1 ) // d = +1
//表示滿足式166中的第一行max中的第一項
{
Gmax1 = t; //更新最大值
Gmax1_idx = i; //得到工作集中第一個βi的索引值i
}
if( !is_lower_bound(i) && (t = G[i]) > Gmax2 ) // d = -1
//表示滿足式166中的第二行max中的第二項
{
Gmax2 = t; //更新最大值
Gmax2_idx = i; //得到工作集中第二個βj的索引值j
}
}
else // y = -1，即式166中的zt＝－1
{
if( !is_upper_bound(i) && (t = -G[i]) > Gmax2 ) // d = +1
//表示滿足式166中的第二行max中的第一項
{
Gmax2 = t; //更新最大值
Gmax2_idx = i; //得到工作集中第二個βj的索引值j
}
if( !is_lower_bound(i) && (t = G[i]) > Gmax1 ) // d = -1
//表示滿足式166中的第一行max中的第二項
{
Gmax1 = t; //更新最大值
Gmax1_idx = i; //得到工作集中第一個βi的索引值i
}
}
}
//為βi和βj賦值
out_i = Gmax1_idx;
out_j = Gmax2_idx;
//式170，判斷迭代是否終止
return Gmax1 + Gmax2 < eps;
}
第二類SVM（ν-SVC和ν-SVR）的選取工作集βi和βj的函數：
bool
CvSVMSolver::select_working_set_nu_svm( int& out_i, int& out_j )
{
// return i,j which maximize -grad(f)^T d , under constraint
// if alpha_i == C, d != +1
// if alpha_i == 0, d != -1
//定義一個最大值
double Gmax1 = -DBL_MAX; // max { -grad(f)_i * d | y_i = +1, d = +1 }
int Gmax1_idx = -1; //初始化ip
double Gmax2 = -DBL_MAX; // max { -grad(f)_i * d | y_i = +1, d = -1 }
int Gmax2_idx = -1; //初始化jp
double Gmax3 = -DBL_MAX; // max { -grad(f)_i * d | y_i = -1, d = +1 }
int Gmax3_idx = -1; //初始化in
double Gmax4 = -DBL_MAX; // max { -grad(f)_i * d | y_i = -1, d = -1 }
int Gmax4_idx = -1; //初始化jn
int i;
//遍歷所有β
for( i = 0; i < alpha_count; i++ )
{
double t;
if( y[i] > 0 ) // y == +1
//第一次由zi＝1這個條件得到ip和jp
{
if( !is_upper_bound(i) && (t = -G[i]) > Gmax1 ) // d = +1
//式167的第一行公式
{
Gmax1 = t; //更新最大值
Gmax1_idx = i; //得到ip
}
if( !is_lower_bound(i) && (t = G[i]) > Gmax2 ) // d = -1
//式167的第二行公式
{
Gmax2 = t; //更新最大值
Gmax2_idx = i; //得到jp
}
}
else // y == -1
//第二次由zi＝－1這個條件得到in和jn
{
if( !is_upper_bound(i) && (t = -G[i]) > Gmax3 ) // d = +1
//式168的第一行公式
{
Gmax3 = t; //更新最大值
Gmax3_idx = i; //得到in
}
if( !is_lower_bound(i) && (t = G[i]) > Gmax4 ) // d = -1
//式168的第二行公式
{
Gmax4 = t; //更新最大值
Gmax4_idx = i; //得到jn
}
}
}
//式171，判斷迭代是否終止
if( MAX(Gmax1 + Gmax2, Gmax3 + Gmax4) < eps )
return 1;
//得到最終的工作集βi和βj
if( Gmax1 + Gmax2 > Gmax3 + Gmax4 ) //式169的第一行公式
{
out_i = Gmax1_idx;
out_j = Gmax2_idx;
}
else //式169的第二行公式
{
out_i = Gmax3_idx;
out_j = Gmax4_idx;
}
return 0;
}
第一類SVM（C-SVC、單類SVM和ε-SVR）的計算決策函數中參數b的函數：
void
CvSVMSolver::calc_rho( double& rho, double& r )
{
int i, nr_free = 0;
double ub = DBL_MAX, lb = -DBL_MAX, sum_free = 0;
//遍歷所有β
for( i = 0; i < alpha_count; i++ )
{
double yG = y[i]*G[i]; //式172的分子中的一項
if( is_lower_bound(i) ) //βi＝0
{
if( y[i] > 0 )
ub = MIN(ub,yG); //式175中min的前一項內容
else
lb = MAX(lb,yG); //式174中max的前一項內容
}
else if( is_upper_bound(i) ) //βi＝C
{
if( y[i] < 0)
ub = MIN(ub,yG); //式175中min的後一項內容
else
lb = MAX(lb,yG); //式174中max的後一項內容
}
else //0＜βi＜C
{
++nr_free; //式172的分母，即計數
sum_free += yG; //式172的分子求和
}
}
//如果nr_free大於0，說明有樣本的βi的值在0和C之間，則利用式172計算ρ；否則利用式173計算ρ
rho = nr_free > 0 ? sum_free/nr_free : (ub + lb)*0.5;
r = 0;
}
第二類SVM（ν-SVC和ν-SVR）的計算決策函數中參數b的函數：
void
CvSVMSolver::calc_rho_nu_svm( double& rho, double& r )
{
int nr_free1 = 0, nr_free2 = 0;
double ub1 = DBL_MAX, ub2 = DBL_MAX;
double lb1 = -DBL_MAX, lb2 = -DBL_MAX;
double sum_free1 = 0, sum_free2 = 0;
double r1, r2;
int i;
//遍歷所有β
for( i = 0; i < alpha_count; i++ )
{
double G_i = G[i]; //得到▽if(β)
if( y[i] > 0 )
{
if( is_lower_bound(i) ) //式178分子中的第二項
ub1 = MIN( ub1, G_i );
else if( is_upper_bound(i) ) //式178分子中的第一項
lb1 = MAX( lb1, G_i );
else //式176
{
++nr_free1; //式176的分母，即計數
sum_free1 += G_i; //式176的分子，求和
}
}
else
{
if( is_lower_bound(i) ) //式179分子中的第二項
ub2 = MIN( ub2, G_i );
else if( is_upper_bound(i) ) //式179分子中的第一項
lb2 = MAX( lb2, G_i );
else //式177
{
++nr_free2; //式177的分母，即計數
sum_free2 += G_i; //式177的分子，求和
}
}
}
//如果nr_free1大於0，說明在zi＝1下有樣本的βi的值在0和C之間，則利用式176計算r1；否則利用式178計算r1
r1 = nr_free1 > 0 ? sum_free1/nr_free1 : (ub1 + lb1)*0.5;
//如果nr_free2大於0，說明在zi＝－1下有樣本的βi的值在0和C之間，則利用式177計算r2；否則利用式179計算r2
r2 = nr_free2 > 0 ? sum_free2/nr_free2 : (ub2 + lb2)*0.5;
rho = (r1 - r2)*0.5; //式180，得到－b
r = (r1 + r2)*0.5; //式180，得到ρ，該變量用於ν-SVC
}
優化那些使用線性核函數（式53）的SVM，目的是用一個支持向量來代表所有的支持向量：
void CvSVM::optimize_linear_svm()
{
// we optimize only linear SVM: compress all the support vectors into one.
if( params.kernel_type != LINEAR ) //判斷是否為線性核函數
return;
//如果是SVC，則得到分類的數量；如果是單類SVM，則class_count為1；如果是SVR，則class_count為0
int class_count = class_labels ? class_labels->cols :
params.svm_type == CvSVM::ONE_CLASS ? 1 : 0;
// df_count為決策函數的數量，在多個分類的SVC中，該值為class_count*(class_count-1)/2，其他情況該值為1
int i, df_count = class_count > 1 ? class_count*(class_count-1)/2 : 1;
CvSVMDecisionFunc* df = decision_func; //賦值決策函數指針
//遍歷所有的決策函數，如果當前決策函數的支持向量的數量不為1，則退出該循環
for( i = 0; i < df_count; i++ )
{
int sv_count = df[i].sv_count;
if( sv_count != 1 )
break;
}
// if every decision functions uses a single support vector;
// it's already compressed. skip it then.
//i為前面for循環中的循環次數索引，如果i等於df_count，說明所有的決策函數中的支持向量的數量都為1個，所以無需再優化處理，則退出該函數
if( i == df_count )
return;
int var_count = get_var_count(); //得到特征屬性的數量
cv::AutoBuffer vbuf(var_count); //為vbuf分配內存
double* v = vbuf; //賦值
//為new_sv變量分配內存，new_sv表示每個決策函數優化處理後的新的支持向量
float** new_sv = (float**)cvMemStorageAlloc(storage, df_count*sizeof(new_sv[0]));
//遍歷所有的決策函數，優化處理每個決策函數
for( i = 0; i < df_count; i++ )
{
//為第i個決策函數的新的支持向量new_sv[i]分配內存
new_sv[i] = (float*)cvMemStorageAlloc(storage, var_count*sizeof(new_sv[i][0]));
float* dst = new_sv[i]; //賦值
memset(v, 0, var_count*sizeof(v[0])); //清零
int j, k, sv_count = df[i].sv_count;
//遍歷當前決策函數的所有支持向量
for( j = 0; j < sv_count; j++ )
{
//得到當前支持向量所對應的樣本
const float* src = class_count > 1 && df[i].sv_index ? sv[df[i].sv_index[j]] : sv[j];
double a = df[i].alpha[j]; //得到當前支持向量的αi
//遍歷該樣本的所有特征屬性，得到一個新的支持向量v＝∑ixiαi
for( k = 0; k < var_count; k++ )
v[k] += src[k]*a;
}
for( k = 0; k < var_count; k++ )
dst[k] = (float)v[k]; //賦值
df[i].sv_count = 1; //此時，只有一個支持向量v
df[i].alpha[0] = 1.; //根據約束條件，只有一個支持向量時，α=1
if( class_count > 1 && df[i].sv_index )
df[i].sv_index[0] = i; //索引賦值
}
sv = new_sv; //新的支持向量
//支持向量的數量，它等於決策函數的數量，因為此時每個決策函數只有一個支持向量
sv_total = df_count;
}
在前面應用get_row函數計算矩陣Q（即式148中的Q=zizjK(xi,xj)）的第i列首地址時，涉及到計算核函數K(xi,xj)，即調用calc函數。在用於SVM對樣本進行預測時，需要計算決策函數，此時也需要計算核函數K(xi,xj)。但兩者還是有區別的，在計算Q時，要用到所有的樣本，而計算決策函數時，只需要用到支持向量即可，也就是說在計算Q時，用於表示支持向量的變量用全體樣本來替代。
下面我們就來介紹calc函數：
void CvSVMKernel::calc( int vcount, int var_count, const float** vecs,
const float* another, Qfloat* results )
// vcount表示支持向量的數量
// var_count表示樣本的特征屬性的數量
// vecs表示具體的支持向量
// another表示核函數所需要的另一個樣本數據，如果是預測，則為預測樣本
//results表示最終的核函數結果
{
const Qfloat max_val = (Qfloat)(FLT_MAX*1e-3);
int j;
//調用calc_func函數
//在實例化CvSVMKernel時，會通過create函數為calc_func的函數指針賦值：當為線性核函數（式53）時，calc_func函數為calc_linear；當為多項式核函數（式54）時，calc_func函數為calc_poly；當為高斯核函數（式56）時，calc_func函數為calc_rbf；當為Sigmoid核函數（式57）時，calc_func函數為calc_sigmoid。這4個函數在後面都有介紹
(this->*calc_func)( vcount, var_count, vecs, another, results );
//遍歷支持向量，確保核函數的向量中不能有太大的元素
for( j = 0; j < vcount; j++ )
{
if( results[j] > max_val )
results[j] = max_val;
}
}
計算線性核函數：
void CvSVMKernel::calc_linear( int vcount, int var_count, const float** vecs,
const float* another, Qfloat* results )
{
//調用calc_non_rbf_base函數，計算α xi·xj＋β，對於線性核函數來說，α＝1，β＝0，該函數在後面會給出講解
calc_non_rbf_base( vcount, var_count, vecs, another, results, 1, 0 );
}
計算多項式核函數：
void CvSVMKernel::calc_poly( int vcount, int var_count, const float** vecs,
const float* another, Qfloat* results )
{
CvMat R = cvMat( 1, vcount, QFLOAT_TYPE, results );
//調用calc_non_rbf_base函數，計算α xi·xj＋β，對於多項式核函數（式54）來說，α＝γ，β＝p，γ為params->gamma，p為params->coef0，該函數在後面會給出講解
calc_non_rbf_base( vcount, var_count, vecs, another, results, params->gamma, params->coef0 );
//最終得到式54，式中的q為params->degree
if( vcount > 0 )
cvPow( &R, &R, params->degree );
}
計算Sigmoid核函數：
void CvSVMKernel::calc_sigmoid( int vcount, int var_count, const float** vecs,
const float* another, Qfloat* results )
{
int j;
//調用calc_non_rbf_base函數，計算－2(γ xi·xj＋p)，對於Sigmoid核函數（式57）來說，α＝－2γ，β＝－2p，γ為params->gamma，p為params->coef0，該函數在後面會給出講解
calc_non_rbf_base( vcount, var_count, vecs, another, results,
-2*params->gamma, -2*params->coef0 );
// TODO: speedup this
for( j = 0; j < vcount; j++ ) //計算式57
{
Qfloat t = results[j]; //得到e的指數部分，即－2(γ xi·xj＋p)
double e = exp(-fabs(t)); //得到e指數
//得到雙曲正切
if( t > 0 )
results[j] = (Qfloat)((1. - e)/(1. + e));
else
results[j] = (Qfloat)((e - 1.)/(e + 1.));
}
}
計算高斯（徑向基函數）核函數：
void CvSVMKernel::calc_rbf( int vcount, int var_count, const float** vecs,
const float* another, Qfloat* results )
{
//定義一個矩陣，作為高斯核函數的結果輸出
CvMat R = cvMat( 1, vcount, QFLOAT_TYPE, results );
double gamma = -params->gamma; //得到式55中的參數－γ
int j, k;
//遍歷所有支持向量
for( j = 0; j < vcount; j++ )
{
const float* sample = vecs[j]; //得到當前支持向量，即樣本數據
double s = 0;
//以4個為一個單位，遍歷當前樣本的特征屬性，計算||xi－xj||
for( k = 0; k <= var_count - 4; k += 4 )
{
double t0 = sample[k] - another[k];
double t1 = sample[k+1] - another[k+1];
s += t0*t0 + t1*t1;
t0 = sample[k+2] - another[k+2];
t1 = sample[k+3] - another[k+3];
s += t0*t0 + t1*t1;
}
//計算不足4個的，也就是剩余的特征屬性的||xi－xj||
for( ; k < var_count; k++ )
{
double t0 = sample[k] - another[k];
s += t0*t0;
}
results[j] = (Qfloat)(s*gamma); //得到－γ||xi－xj||
}
if( vcount > 0 )
cvExp( &R, &R ); //得到最終的結果，即式56
}
除了calc_rbf函數以外，calc_linear函數，calc_poly函數和calc_sigmoid函數都會調用calc_non_rbf_base函數，因為這3個核函數都需要計算xi·xj：
void CvSVMKernel::calc_non_rbf_base( int vcount, int var_count, const float** vecs,
const float* another, Qfloat* results,
double alpha, double beta )
{
int j, k;
//遍歷所有支持向量
for( j = 0; j < vcount; j++ )
{
const float* sample = vecs[j]; //得到當前的支持向量，即樣本數據
double s = 0;
//以4個為一個單位，遍歷當前樣本的特征屬性，計算xi·xj
for( k = 0; k <= var_count - 4; k += 4 )
s += sample[k]*another[k] + sample[k+1]*another[k+1] +
sample[k+2]*another[k+2] + sample[k+3]*another[k+3];
//計算不足4個的，也就是剩余的特征屬性的xi·xj
for( ; k < var_count; k++ )
s += sample[k]*another[k];
//最終得到α xi·xj＋β
results[j] = (Qfloat)(s*alpha + beta);
}
}
下面介紹SVM預測樣本函數predict。該函數有許多形式，如：
float CvSVM::predict(const Mat& sample,bool returnDFVal=false )
float CvSVM::predict(const CvMat* sample,bool returnDFVal=false )
float CvSVM::predict(const CvMat* samples,CvMat* results)
其中，sample表示需要預測的樣本數據，returnDFVal定義該函數的返回類型，為true，並且是兩類分類問題時，該函數返回決策函數中sgn函數內的具體值，否則該函數返回分類標簽（SVC），或返回估計函數（SVR），results表示相對應樣本的預測輸出，如果只預測一個樣本，則該函數返回預測結果，如果預測多個樣本，則必須使用results參數來返回預測結果。
不管哪種形式的predict函數，最終都會調用下面這個函數：
float CvSVM::predict( const float* row_sample, int row_len, bool returnDFVal ) const
// row_sample表示待預測的一個樣本
// row_len表示該樣本的特征屬性的數量
//函數返回為預測結果
{
assert( kernel ); //確保SVM模型中核函數數據形式的正確
assert( row_sample ); //確保預測樣本數據形式的正確
int var_count = get_var_count(); //得到SVM模型中樣本的特征屬性的數量
//確保SVM模型的樣本和預測樣本的特征屬性的數量相同
assert( row_len == var_count );
(void)row_len;
//如果是SVC，class_count為分類的數量；如果是單類SVM，class_count為1；如果是SVR，class_count為0
int class_count = class_labels ? class_labels->cols :
params.svm_type == ONE_CLASS ? 1 : 0;
float result = 0; //表示預測結果
cv::AutoBuffer _buffer(sv_total + (class_count+1)*2); //分配一塊內存空間
float* buffer = _buffer;
if( params.svm_type == EPS_SVR || //ε-SVR類型
params.svm_type == NU_SVR || //ν-SVR類型
params.svm_type == ONE_CLASS ) //單類SVM類型
{
CvSVMDecisionFunc* df = (CvSVMDecisionFunc*)decision_func; //得到決策函數
int i, sv_count = df->sv_count; //sv_count表示支持向量的數量
double sum = -df->rho; //得到決策函數的參數b
//計算核函數
kernel->calc( sv_count, var_count, (const float**)sv, row_sample, buffer );
//遍歷所有的支持向量，由決策函數得到最終的預測結果
for( i = 0; i < sv_count; i++ )
sum += buffer[i]*df->alpha[i];
//如果是單類SVM，則對sum取sgn，即式90
result = params.svm_type == ONE_CLASS ? (float)(sum > 0) : (float)sum;
}
else if( params.svm_type == C_SVC || //C-SVC類型
params.svm_type == NU_SVC ) //ν-SVC類型
{
CvSVMDecisionFunc* df = (CvSVMDecisionFunc*)decision_func; //得到決策函數
int* vote = (int*)(buffer + sv_total); //表示記錄投票結果
int i, j, k;
//為vote開辟內存並清零
memset( vote, 0, class_count*sizeof(vote[0]));
//計算核函數
kernel->calc( sv_total, var_count, (const float**)sv, row_sample, buffer );
double sum = 0.;
for( i = 0; i < class_count; i++ ) //遍歷所有分類類別
{
//對不重復的兩個分類進行比較
for( j = i+1; j < class_count; j++, df++ )
{
sum = -df->rho; //得到決策函數的參數b
int sv_count = df->sv_count;
//遍歷所有的支持向量，由決策函數得到最終的預測結果
for( k = 0; k < sv_count; k++ )
sum += df->alpha[k]*buffer[df->sv_index[k]];
vote[sum > 0 ? i : j]++; //統計投票結果
}
}
//遍歷所有分類類別，得到票數最多的那個分類類別
for( i = 1, k = 0; i < class_count; i++ )
{
if( vote[i] > vote[k] )
k = i; //k表示票數最多的那個分類類別
}
//如果returnDFVal為true，並且是2類的SVM，則result為決策函數中sgn函數內的值，否則result為預測的分類標簽
result = returnDFVal && class_count == 2 ? (float)sum : (float)(class_labels->data.i[k]);
}
else //不是以上5種SVM類型，則提示錯誤信息
CV_Error( CV_StsBadArg, "INTERNAL ERROR: Unknown SVM type, "
"the SVM structure is probably corrupted" );
return result; //返回預測結果
}
應用實例
下面我們給出一個具體的SVM應用實例。本次的實例來源於http://archive.ics.uci.edu/ml/中的risi數據，目的是用於判斷樣本是屬於哪類植物：setosa，versicolor，virginica。每類植物各選擇20個樣本進行訓練，而每個樣本具有以下4個特征屬性：花萼長，花萼寬，花瓣長，花瓣寬。
#include "opencv2/core/core.hpp" #include "opencv2/highgui/highgui.hpp" #include "opencv2/imgproc/imgproc.hpp" #include "opencv2/ml/ml.hpp" #includeusing namespace cv; using namespace std; int main( int argc, char** argv ) { //60個訓練樣本 double trainingData[60][4]={{5.1,3.5,1.4,0.2}, {4.9,3.0,1.4,0.2}, {4.7,3.2,1.3,0.2}, {4.6,3.1,1.5,0.2}, {5.0,3.6,1.4,0.2}, {5.4,3.9,1.7,0.4}, {4.6,3.4,1.4,0.3}, {5.0,3.4,1.5,0.2}, {4.4,2.9,1.4,0.2}, {4.9,3.1,1.5,0.1}, {5.4,3.7,1.5,0.2}, {4.8,3.4,1.6,0.2}, {4.8,3.0,1.4,0.1}, {4.3,3.0,1.1,0.1}, {5.8,4.0,1.2,0.2}, {5.7,4.4,1.5,0.4}, {5.4,3.9,1.3,0.4}, {5.1,3.5,1.4,0.3}, {5.7,3.8,1.7,0.3}, {5.1,3.8,1.5,0.3}, {7.0,3.2,4.7,1.4}, {6.4,3.2,4.5,1.5}, {6.9,3.1,4.9,1.5}, {5.5,2.3,4.0,1.3}, {6.5,2.8,4.6,1.5}, {5.7,2.8,4.5,1.3}, {6.3,3.3,4.7,1.6}, {4.9,2.4,3.3,1.0}, {6.6,2.9,4.6,1.3}, {5.2,2.7,3.9,1.4}, {5.0,2.0,3.5,1.0}, {5.9,3.0,4.2,1.5}, {6.0,2.2,4.0,1.0}, {6.1,2.9,4.7,1.4}, {5.6,2.9,3.6,1.3}, {6.7,3.1,4.4,1.4}, {5.6,3.0,4.5,1.5}, {5.8,2.7,4.1,1.0}, {6.2,2.2,4.5,1.5}, {5.6,2.5,3.9,1.1}, {6.3,3.3,6.0,2.5}, {5.8,2.7,5.1,1.9}, {7.1,3.0,5.9,2.1}, {6.3,2.9,5.6,1.8}, {6.5,3.0,5.8,2.2}, {7.6,3.0,6.6,2.1}, {4.9,2.5,4.5,1.7}, {7.3,2.9,6.3,1.8}, {6.7,2.5,5.8,1.8}, {7.2,3.6,6.1,2.5}, {6.5,3.2,5.1,2.0}, {6.4,2.7,5.3,1.9}, {6.8,3.0,5.5,2.1}, {5.7,2.5,5.0,2.0}, {5.8,2.8,5.1,2.4}, {6.4,3.2,5.3,2.3}, {6.5,3.0,5.5,1.8}, {7.7,3.8,6.7,2.2}, {7.7,2.6,6.9,2.3}, {6.0,2.2,5.0,1.5} }; Mat trainingDataMat(60, 4, CV_32FC1, trainingData); //訓練樣本所對應的類別，S表示setosa，V表示versicolor，R表示virginica float responses[60] = {'S','S','S','S','S','S','S','S','S','S','S','S','S','S','S','S','S','S','S','S', 'V','V','V','V','V','V','V','V','V','V','V','V','V','V','V','V','V','V','V','V', 'R','R','R','R','R','R','R','R','R','R','R','R','R','R','R','R','R','R','R','R'}; Mat responsesMat(60, 1, CV_32FC1, responses); //設置SVM參數 CvSVMParams params; params.svm_type = CvSVM::C_SVC; //SVM類型為C-SVC params.C = 10.0; //C參數設置為10 params.kernel_type = CvSVM::RBF; //核函數為高斯核函數 params.gamma = 8.0; //高斯核函數中的γ參數設置為8 //迭代的終止條件 params.term_crit = cvTermCriteria(CV_TERMCRIT_EPS, 1000, FLT_EPSILON); //建立SVM模型 CvSVM svm; svm.train(trainingDataMat, responsesMat, Mat(), Mat(), params); //預測樣本數據 double sampleData[4]={ 6.7, 3.1, 4.7, 1.5}; Mat sampleMat(4, 1, CV_32FC1, sampleData); float r = svm.predict(sampleMat); //預測結果 cout<
qq空間打賞紅包怎麼領 qq空間打賞紅包在哪領取
QQ空間打賞紅包是手機QQ最近新推出的一個功能，這個打賞紅包功能可以讓你給QQ空間中發表優質內容的人打賞紅包，如果你看到好友發了一條說說可以試試這個QQ空間
Activity啟動清空原任務棧
若有這樣的需求或場景，要求每次啟動Activity時都清空原有的任務棧，也就是finish掉原任務棧中的所有Activity，有沒有一種鸠占鵲巢的趕腳？下面介紹的這個方法
為Android app提供資源
您應該始終外部化應用資源，例如圖像和代碼中的字符串，這樣有利於您單獨維護這些資源。 此外，您還應該為特定設備配置提供備用資源，方法是將它們分組到專門命名的資源目錄中。 在
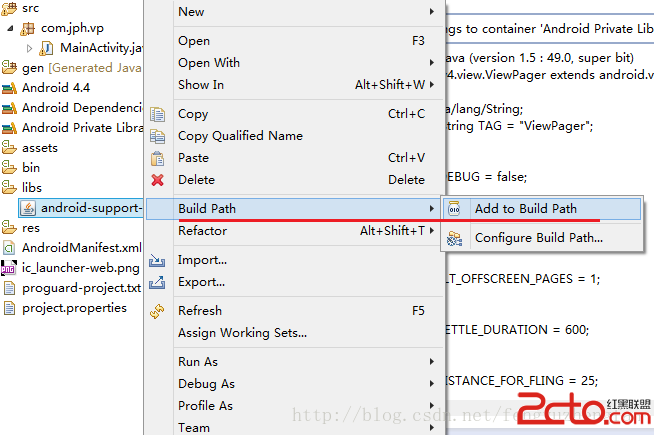Android關聯源碼support-v4,v7,v13源碼
在Android實際開發過程中往往會遇到使用v4,v7或v13兼容包中的一些類如ViewPager,Fargment等，但卻無法關聯源碼。 網上有很多解決
