編輯：關於Android編程
本文主要記錄了Launcher3拖動時的流程和代碼記錄，在桌面圖標拖動時會引起圖標的重排，拖動時受影響的圖標在文中由item或cell來表示。
mTouchFeedbackView為點擊按下時圖標表面一層透明灰色動畫效果，這個動畫效果在Celllayout中，在構造函數中addView加入，BubbleTextView 中 setStayPressed方法調用這個動畫效果，在點擊圖標時呈現，下圖就是我把Wallpaper改變成純白色，更改動畫位置，這樣效果很明顯。
addView(mTouchFeedbackView, (int) (grid.cellWidthPx * 1.5), (int) (grid.cellHeightPx * 1.5));
addView(mShortcutsAndWidgets);拖動時受影響的Item有一個搖動的(shake)動畫，這個動畫效果是通過ReorderPreviewAnimation和mShakeAnimators實現，受影響的item由ItemConfiguration管理，Celllayout-completeAndClearReorderPreviewAnimations方法播放動畫，在適當時機調用。這個動畫比較有意思，單純的線性動畫沒有這種效果，看了代碼才發現用到了貝塞爾曲線線性方程，這部分代碼主要在Celllayout中。
Celllayout的boolean[][] mOccupied存儲桌面圖標布局中是否有圖標占位，存在則為true，該對象在CellLayout的addViewToCellLayout方法賦值，這個方法在Workspace-addInScreen方法中調用，而桌面初始化時的bind過程會一直調用到這個方法。
DragLayer是Launcher3中處理拖動圖標事件時自定義View，DragController的注釋為：發起一個在一個View內或在幾個View之間拖動事件的類。從名字可以看出這個類是一個調節者或控制者。
在DragLayer-onInterceptTouchEvent方法將事件給DragController-onInterceptTouchEvent方法處理。拖動圖標的事件開始處理時，會一直調用到DragController-startDrag方法，此時，startDrag裡將mDragging置為true,而DragController-onInterceptTouchEvent返回mDragging,此時截斷事件傳遞，當前View處理觸摸事件。類似的，DragLayer的onTouchEent方法也將事件給DragController的onTouchEent方法處理。
handleMoveEvent方法為處理觸摸事件的主要方法，在handleMoveEvent方法中調用findDropTarget取的當前的具體的DropTarget對象，DragController中有一個mDropTargets鏈表，這個鏈表中在桌面的加載和操作會包含進來具體DropTarget對象，在Launcher3中，實現DropTarget類的有Folder和Workspace等，這個interface抽象了拖動時落點對象。DropTarget-isDropEnabled方法，表示當前這個落點View是否可以Drop，當該方法返回false時，顯然是不能將拖動的Object放到這裡來的。checkTouchMove方法檢查拖動時的狀態，根據拖動時DropTarget之間的關系調用DropTarget聲明的onDrop，onDragEnter,onDragExit,onDragOver方法進行視圖的演示，最後調用checkScrollState方法，這個方法主要是對拖動時的翻頁進行判斷處理。
根據checkTouchMove方法，在Workspace中開始拖動圖標時，圖標開始時在Workspace中，此時DropTarget也為Workspace，所以剛開始時調用Workspace的onDragEnter方法，緊接著調用Workspace的onDragOver方法。而onDragExit方法的調用時機為拖動的Cell離開當前Target，當前Target變為mLastDropTarget，又沒有進入一個有效的Target時。
Workspace的onDragEnter方法，這個方法比較簡單，對Workspace的拖動時的涉及到的變量進行了初始化。
Workspace的onDragOver方法，在Workspace中有一個mDragViewVisualCenter變量，根據字面理解，這個變量是拖動對象的視覺中心位置，由getDragViewVisualCenter方法計算而來，在對拖動處理時多處使用，此外拖動的時候也要判斷當前位置Layout的是處於翻動的頁面還是Hotseat中，確定mDragTargetLayout。接著findNearestArea方法根據mDragViewVisualCenter先大致當前的落點，findNearestArea方法會調用到Celllayout的findNearestArea方法，根據不同情況在調用的過程中會分別考慮和不考慮當前頁面的其他item的占用情況。確定了可能的落點後首先對Folder情況進行處理，分別為新建和加入已有的Folder兩種，然後是落點已經被其他的Item占據的情況，這裡調用performReorder方法處理，這個方法相當長，拖動過程中和結束拖動放下時的onDrag方法中都會調用這個方法，拖動過程中圖標的重排效果就是在此方法中實現的。Workspace的onDragExit方法，根據上面onDragExit的調用時機，這裡主要確定拖動圖標離開有效DragTarget時最後的落點。
根據DragController的onTouchEent方法，觸摸事件為MotionEvent.ACTION_UP時，拖動事件結束，這時有兩種可能：當滿足快速向上扔時，刪除拖動的item，isFlingingToDelete方法判斷條件是否滿足。如果不滿足扔的條件，調用drop方法，drop方法調用DropTarget的acceptDrop方法，判斷該Drop事件是否發生，依此調用DropTarget的onDrop方法。
Workspace-onDrop()流程，方法參數為DropTarget-DragObject對象，首先計算拖動View的視覺中心mDragViewVisualCenter，dropTargetLayout為Drop的Celllayout對象，下一步判斷當前是否在Hotseat上，求出相對於dropTargetLayout的視覺中心坐標。如果DragObject-dragSource！=Worspace，轉而調用onDropExternal()，否則繼續處理onDrop()的內容。接著調用findNearestArea方法球drop的xy的值，Workspace-findNearestArea()調用到CellLayout-findNearestArea(),該方法是一個重要的方法，作用是找到離落點最近距離cell，其中有一個boolean參數ignoreOccupied，當ignoreOccupied為false時，尋找cell時不考慮已經占據的區域，為true時考慮。
接下來開始處理落點和文件夾的關系,如果落點處可以合成一個Folder，調用Workspace-createUserFolderIfNecessary()方法，如果拖動的圖標可以加進一個文件夾，則調用Workspace-addToExistingFolderIfNecessary()方法。如果不滿足文件夾的條件，則調用CellLayout-performReorder方法，這個方法就是處理拖動圖標時，如果當前落點被占據時，擠開當前圖標的效果。
AppWidget可能在拖動時發生縮小，因此會調用AppWidgetResizeFrame-updateWidgetSizeRanges方法，拖動時可能落點在別的頁面，所以還會有頁面滑動的效果。如果滿足則更新位置，保存新的位置信息到數據庫中，播放動畫效果，否則彈回原來位置。
acceptDrop方法的調用過程和邏輯和onDrop方法差不多，需要注意的是調用performReorder方法時mode參數不同。
除了DropTarget，WorkSpace還implements了DragController.DragListener，DragCtroller中存在一個mListeners鏈表，在桌面加載時會將相應的對象加進來，比如Workspace在Launcher的setupViews方法中加入。這個接口聲明了onDragStart方法和onDragEnd方法,上面說過開始拖動時調用DragController的startDrag方法,startDrag方法中依次調用mListeners中對象的onDragStart方法，這裡處理的是開始拖動時桌面受影響的View對象，比如剛開始拖動時Workspace有一些提示效果，搜索刪除按鈕(SearchDropTargetBar)會由搜索界面變為刪除等，這些View對象都是繼承了這個借口的。除此外，startDrag方法還顯示了拖動item的DragView。Workspace的onDragStart方法處理了一些界面相關的操作，比如鎖定屏幕方向，生成額外的空白頁等。onDragEnd方法即為相反的操作。
Workspace還實現了一個拖動相關的接口為DragSource接口，這個接口定義了拖動可以從它本身開始的對象，就是可以從Workspace開始拖動一個圖標，DragSorce聲明了一系列拖動時判斷條件或某種狀態回調的方法。
findNearestArea方法，這個在拖動過程出鏡頻率相當高。
/**
* Find a vacant area that will fit the given bounds nearest the requested
* cell location. Uses Euclidean distance to score multiple vacant areas.
*/
int[] findNearestArea(int pixelX, int pixelY, int minSpanX, int minSpanY, int spanX, int spanY,
View ignoreView, boolean ignoreOccupied, int[] result, int[] resultSpan,
boolean[][] occupied) {
//初始化一個mCountX*mCountY的棧
lazyInitTempRectStack();
// mark space take by ignoreView as available (method checks if ignoreView is null)
//此時occupied為mOccupied,這裡將ignoreView的位置置為false,即忽略當前位置View
markCellsAsUnoccupiedForView(ignoreView, occupied);
// For items with a spanX / spanY > 1, the passed in point (pixelX, pixelY) corresponds
// to the center of the item, but we are searching based on the top-left cell, so
// we translate the point over to correspond to the top-left.
// 即左上角cell的中心pixelX -= (mCellWidth*span + mWidthGap*(spanX-1))/2-mCellWidth/2
pixelX -= (mCellWidth + mWidthGap) * (spanX - 1) / 2f;
pixelY -= (mCellHeight + mHeightGap) * (spanY - 1) / 2f;
// Keep track of best-scoring drop area
final int[] bestXY = result != null ? result : new int[2];
double bestDistance = Double.MAX_VALUE;
final Rect bestRect = new Rect(-1, -1, -1, -1);
final Stack validRegions = new Stack();
final int countX = mCountX;
final int countY = mCountY;
if (minSpanX <= 0 || minSpanY <= 0 || spanX <= 0 || spanY <= 0 ||
spanX < minSpanX || spanY < minSpanY) {
return bestXY;
}
for (int y = 0; y < countY - (minSpanY - 1); y++) {
inner:
for (int x = 0; x < countX - (minSpanX - 1); x++) {
int ySize = -1;
int xSize = -1;
//為true時代表要考慮已經被占據的位置
//先尋找符合minSpanX和minSpanY的位置
//然後向分x，y方向向外擴大，試探當前位置最大的可能性
//findConfigurationNoShuffle方法調用時為true
if (ignoreOccupied) {
// First, let's see if this thing fits anywhere
for (int i = 0; i < minSpanX; i++) {
for (int j = 0; j < minSpanY; j++) {
if (occupied[x + i][y + j]) {
continue inner;
}
}
}
xSize = minSpanX;
ySize = minSpanY;
// We know that the item will fit at _some_ acceptable size, now let's see
// how big we can make it. We'll alternate between incrementing x and y spans
// until we hit a limit.
boolean incX = true;
//為true停止
boolean hitMaxX = xSize >= spanX;
boolean hitMaxY = ySize >= spanY;
while (!(hitMaxX && hitMaxY)) {
if (incX && !hitMaxX) {
for (int j = 0; j < ySize; j++) {
if (x + xSize > countX -1 || occupied[x + xSize][y + j]) {
// We can't move out horizontally
hitMaxX = true;
}
}
// We know that the item will fit at _some_ acceptable size, now let's see
// how big we can make it. We'll alternate between incrementing x and y spans
// until we hit a limit.
boolean incX = true;
//為true停止
boolean hitMaxX = xSize >= spanX;
boolean hitMaxY = ySize >= spanY;
while (!(hitMaxX && hitMaxY)) {
if (incX && !hitMaxX) {
for (int j = 0; j < ySize; j++) {
if (x + xSize > countX -1 || occupied[x + xSize][y + j]) {
// We can't move out horizontally
hitMaxX = true;
}
}
if (!hitMaxX) {
xSize++;
}
} else if (!hitMaxY) {
for (int i = 0; i < xSize; i++) {
if (y + ySize > countY - 1 || occupied[x + i][y + ySize]) {
// We can't move out vertically
hitMaxY = true;
}
}
if (!hitMaxY) {
ySize++;
}
}
//為true或大於等於span
hitMaxX |= xSize >= spanX;
hitMaxY |= ySize >= spanY;
incX = !incX;
}
incX = true;
hitMaxX = xSize >= spanX;
hitMaxY = ySize >= spanY;
}
//求(x, y)的點的坐標
final int[] cellXY = mTmpXY;
cellToCenterPoint(x, y, cellXY);
// We verify that the current rect is not a sub-rect of any of our previous
// candidates. In this case, the current rect is disqualified in favour of the
// containing rect.
Rect currentRect = mTempRectStack.pop();
currentRect.set(x, y, x + xSize, y + ySize);
boolean contained = false;
for (Rect r : validRegions) {
if (r.contains(currentRect)) {
contained = true;
break;
}
}
validRegions.push(currentRect);
double distance = Math.sqrt(Math.pow(cellXY[0] - pixelX, 2)
+ Math.pow(cellXY[1] - pixelY, 2));
if ((distance <= bestDistance && !contained) ||
currentRect.contains(bestRect)) {
bestDistance = distance;
bestXY[0] = x;
bestXY[1] = y;
if (resultSpan != null) {
resultSpan[0] = xSize;
resultSpan[1] = ySize;
}
bestRect.set(currentRect);
}
}
}
// re-mark space taken by ignoreView as occupied
// 恢復occupied的值
markCellsAsOccupiedForView(ignoreView, occupied);
// Return -1, -1 if no suitable location found
if (bestDistance == Double.MAX_VALUE) {
bestXY[0] = -1;
bestXY[1] = -1;
}
recycleTempRects(validRegions);
return bestXY;
} 在後面拖動時具體執行桌面重排時會調用到findNearestArea方法的重載方法，還會權衡建議的方向向量。
rearrangementExists方法：
參數solution為ItemConfiguration對象，ItemConfiguration保存了當前桌面各個item的情況。首先確定拖動View的Rect，使用Rect.intersects方法，得出soulution的intersectingViews列表，這裡是拖動時影響到的item。接下來實現具體的方案，根據注釋，首先找出符合推力的方案attemptPushInDirection方法，拖動時，一個被推出當前位置item也會擠開別的item，如果失敗，addViewsToTempLocation方法，嘗試受影響的iew整塊移動，如果還是不想，遍歷mIntersectingViews，addViewToTempLocation方法分別嘗試放置到新位置。
attemptPushInDirection方法：
若xy方向上均有作用力，先pushViewsToTempLocation()移動x軸，再移動y軸，若正方向上移動失敗，換方向，若只有一個方向有作用力，以以下順序推動，正方向，反方向，xy軸互換，xy軸互換反方向。確定方向後，調用pushViewsToTempLocation方法。
pushViewsToTempLocation方法：
這個方法裡初始化了ViewCluster對象,這個類有四個數組(leftEdge，rightEdge，topEdge和bottomEdge)記錄了上下左右邊上當前影響的Views的邊界位置，用來精確的表示一串view的邊界，以便於在拖動時操作View的情況。
![ViewCluster](https://www.android5.online/Android/UploadFiles_5356/201702/2017022315275537.png "\")
例如上圖4*4的WZ喎?/kf/ware/vc/" target="_blank" class="keylink">vcmtzcGFjZaOsyOe5+83Ptq/Su7j2aXRlbbTT09K/v738yrHW03dpZGdldMqxo6zKsdbTd2lkZ2V0vs3Oqsrc07DP7LXEVmlld6OstMvKsVZpZXdDbHVzdGVyttTP89a709DSu7j2Vmlld6Osy/y1xMvEuPax373nyv3X6bfWsfDOqnsxLDEsLTEsLTF9LHsyLDIsLTEsLTF9LHstMSwwLDAsLTF9us17LTEsMSwxLC0xfaOss/XKvLuvyrHOqi0xo6y0+rHtuMPOu9bDw7vT0Mrc07DP7LXEVmlld6GjPC9wPgoKPHA+ytfPyLj5vt3NxsGmz/LBv7XEt73P8rzGy+O1scewytzTsM/stcSx373nus2xu83Gv6q1xHZpZXe1xNLGtq++4MDrcHVzaERpc3RhbmNlo6xWaWV3Q2x1c3RlcrXEc29ydENvbmZpZ3VyYXRpb25Gb3JFZGdlUHVzaLe9t6i4+b7dtbHHsLHfvee9q83Ptq/Kscrc07DP7LXEVmlld8XQts/PyLrzytzTsM/stcS0ztDyxcXQ8qGjzca2r8qxo6zF9rW9YWxsIGFwcLC0xaWjrLy0Y2FuUmVvcmRlcs6qZmFsc2WjrM3Gtq/Kp7DcoaPNxravyrGx6cD60tTFxbrD0PK1xMHQse2jrLX308Npc1ZpZXdUb3VjaGluZ0VkZ2W3vbeoxdC2z7Wxx7BWaWV3yse38b3TtKW1vbWxx7DK3NOwz+xWaWV3vK+jrHRydWXU8rzTvfjAtKOs0ru0zs3Gtq/Su7j2taXOu77gwOujrNK71rHNxrW9xL+x6s671sOjrM3Ptq/KsdOwz+y1xHZpZXe+zdXi0fnSu7LjsuPAqbTzobC40Mi+obGho83Ptq+94cr4uvOjrMXQts+94bn7yse38bOsuf2x373no6yyu7rPuPHU8nJlc3RvcmW3tbvYx7DXtMysoaM8L3A+Cgo8cD5hZGRWaWV3c1RvVGVtcExvY2F0aW9ut723qCA8YnI+CmJvdW5kaW5nUmVjdM6qy/nT0M/gudh2aWV3y/nVvLXEcmVjdMq508N1bmlvbre9t6jBqrrPtcRSZWN0o6zU2dPD0ru49mJvb2xlYW62/s6syv3X6bHtyr7G5L6ryLe1xNW8vt3H6b/2o6zU2bX308PJz8Pmy/nLtbXEZmluZE5lYXJlc3RBcmVh1tjU2Le9t6jH87P2wuTPwsf40/Kho2FkZFZpZXdUb1RlbXBMb2NhdGlvbre9t6jA4MvGoaM8L3A+Cgo8cD7G5Mv7RHJvcFRhcmdldLbUz/O6zVdvcmtzcGFjZbTzzazQodLso6y4+b7dsrvNrLXEx+m+sLmmxNy/ycTcz7i92snPu+HT0LK7zayhozwvcD4KCjxoMyBpZD0="數學基礎">數學基礎
數量積 isFlingingToDelete方法，findNearestArea方法，這裡用於判斷方向是否符合。
維基百科：https://zh.wikipedia.org/wiki/%E6%95%B0%E9%87%8F%E7%A7%AF
三角函數 computeDirectionVector方法，這裡計算具體的推動方向
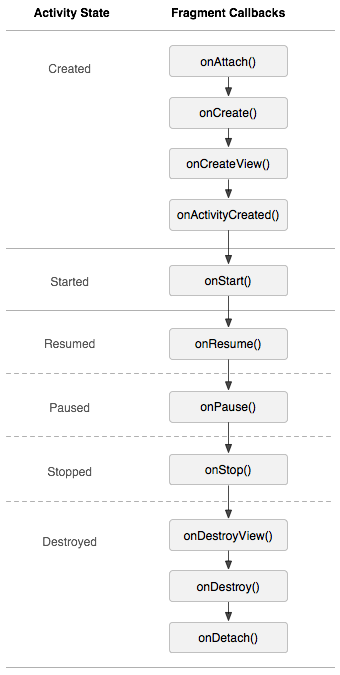深入淺析 Android Fragment(上篇)
自從Fragment出現，曾經有段時間，感覺大家談什麼都能跟Fragment談上關系，做什麼都要問下Fragment能實現不~~~哈哈，是不是有點過~~~為了讓界面可以在
框架模式MVC與MVP在Android中的應用
很多人在開發Android項目時沒有考慮過架構模式的問題，以至於隨著項目的增大，Activty或者Fragment中代碼也會越來越多，導致項目的維護變的越來越復雜。然而在
Android教程-從零開始一步一步接入SDK
從零開始一步一步接入SDK 本篇博客想總結一下筆者在接入手游渠道SDK的一些經驗方法，為想接入手游渠道或者想學習如何接入SDK的童鞋們提供一個參考。本篇博客基於Andr
Unity3D之導出的Apk安裝失敗
最近用Unity3D導出Apk到手機上出現的問題，開始可以正常安裝到手機上。然而在我將導出的Apk在電腦的模擬機運行了幾次之後，再導入到手機上卻一直安裝失敗。後來在Pla
Android Touch系統簡介（二）:實例詳解onInterceptTouchEvent與onTouchEvent的調用過程
上一篇文章主要講述了Android的TouchEvent的分發過程，其中
