編輯:關於Android編程
題意就是給一個數,然後求這個數的所有因子中組成的最大的一個子集,其中1和本身除外,使得在這個子集中元素兩兩互素,求最大子集的元素個
數,並且求出和最大的值。
找規律就不難發現其實答案就是先大數分解n,例如,180=2^2*3^2*5,那麼就輸出3 18 ,這兩個數分別是素因子的個數和2^2,3^2,5的和。
[cpp]
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <algorithm>
#include <iostream>
const int Times=10;
const int N=550;
using namespace std;
typedef unsigned __int64 LL;
LL ct,cnt;
LL fac[N],num[N];
LL gcd(LL a,LL b)
{
return b? gcd(b,a%b):a;
}
LL multi(LL a,LL b,LL m)
{
LL ans=0;
while(b)
{
if(b&1)
{
ans=(ans+a)%m;
b--;
}
b>>=1;
a=(a+a)%m;
}
return ans;
}
LL quick_mod(LL a,LL b,LL m)
{
LL ans=1;
a%=m;
while(b)
{
if(b&1)
{
ans=multi(ans,a,m);
b--;
}
b>>=1;
a=multi(a,a,m);
}
return ans;
}
bool Miller_Rabin(LL n)
{
if(n==2) return true;
if(n<2||!(n&1)) return false;
LL a,m=n-1,x,y;
int k=0;
while((m&1)==0)
{
k++;
m>>=1;
}
for(int i=0;i<Times;i++)
{
a=rand()%(n-1)+1;
x=quick_mod(a,m,n);
for(int j=0;j<k;j++)
{
y=multi(x,x,n);
if(y==1&&x!=1&&x!=n-1) return false;
x=y;
}
if(y!=1) return false;
}
return true;
}
LL Pollard_rho(LL n,LL c)
{
LL x,y,d,i=1,k=2;
y=x=rand()%(n-1)+1;
while(true)
{
i++;
x=(multi(x,x,n)+c)%n;
d=gcd((y-x+n)%n,n);
if(1<d&&d<n) return d;
if(y==x) return n;
if(i==k)
{
y=x;
k<<=1;
}
}
}
void find(LL n,int c)
{
if(n==1) return;
if(Miller_Rabin(n))
{
fac[ct++]=n;
return ;
}
LL p=n;
LL k=c;
while(p>=n) p=Pollard_rho(p,c--);
find(p,k);
find(n/p,k);
}
int main()
{
int t;
LL n,ans;
scanf("%d",&t);
while(t--)
{
scanf("%I64u",&n);
ct=0;
find(n,120);
sort(fac,fac+ct);
num[0]=1;
int k=1;
for(int i=1;i<ct;i++)
{
if(fac[i]==fac[i-1])
++num[k-1];
else
{
num[k]=1;
fac[k++]=fac[i];
}
}
cnt=k;
LL ret=0;
for(int i=0;i<cnt;i++)
{
LL temp=1;
for(int j=0;j<num[i];j++)
temp*=fac[i];
ret+=temp;
}
if(cnt==1) ret/=fac[0];
printf("%I64u %I64u\n",cnt,ret);
}
return 0;
}
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <algorithm>
#include <iostream>
const int Times=10;
const int N=550;
using namespace std;
typedef unsigned __int64 LL;
LL ct,cnt;
LL fac[N],num[N];
LL gcd(LL a,LL b)
{
return b? gcd(b,a%b):a;
}
LL multi(LL a,LL b,LL m)
{
LL ans=0;
while(b)
{
if(b&1)
{
ans=(ans+a)%m;
b--;
}
b>>=1;
a=(a+a)%m;
}
return ans;
}
LL quick_mod(LL a,LL b,LL m)
{
LL ans=1;
a%=m;
while(b)
{
if(b&1)
{
ans=multi(ans,a,m);
b--;
}
b>>=1;
a=multi(a,a,m);
}
return ans;
}
bool Miller_Rabin(LL n)
{
if(n==2) return true;
if(n<2||!(n&1)) return false;
LL a,m=n-1,x,y;
int k=0;
while((m&1)==0)
{
k++;
m>>=1;
}
for(int i=0;i<Times;i++)
{
a=rand()%(n-1)+1;
x=quick_mod(a,m,n);
for(int j=0;j<k;j++)
{
y=multi(x,x,n);
if(y==1&&x!=1&&x!=n-1) return false;
x=y;
}
if(y!=1) return false;
}
return true;
}
LL Pollard_rho(LL n,LL c)
{
LL x,y,d,i=1,k=2;
y=x=rand()%(n-1)+1;
while(true)
{
i++;
x=(multi(x,x,n)+c)%n;
d=gcd((y-x+n)%n,n);
if(1<d&&d<n) return d;
if(y==x) return n;
if(i==k)
{
y=x;
k<<=1;
}
}
}
void find(LL n,int c)
{
if(n==1) return;
if(Miller_Rabin(n))
{
fac[ct++]=n;
return ;
}
LL p=n;
LL k=c;
while(p>=n) p=Pollard_rho(p,c--);
find(p,k);
find(n/p,k);
}
int main()
{
int t;
LL n,ans;
scanf("%d",&t);
while(t--)
{
scanf("%I64u",&n);
ct=0;
find(n,120);
sort(fac,fac+ct);
num[0]=1;
int k=1;
for(int i=1;i<ct;i++)
{
if(fac[i]==fac[i-1])
++num[k-1];
else
{
num[k]=1;
fac[k++]=fac[i];
}
}
cnt=k;
LL ret=0;
for(int i=0;i<cnt;i++)
{
LL temp=1;
for(int j=0;j<num[i];j++)
temp*=fac[i];
ret+=temp;
}
if(cnt==1) ret/=fac[0];
printf("%I64u %I64u\n",cnt,ret);
}
return 0;
}
 Android使用ViewDragHelper實現仿QQ6.0側滑界面(一)
Android使用ViewDragHelper實現仿QQ6.0側滑界面(一)
QQ是大家離不開的聊天工具,方便既實用,自從qq更新至6.0之後,側滑由原來的劃出後主面板縮小變成了左右平滑,在外觀上有了很大的提升,於是我就是嘗試理解下裡面的各種邏輯,
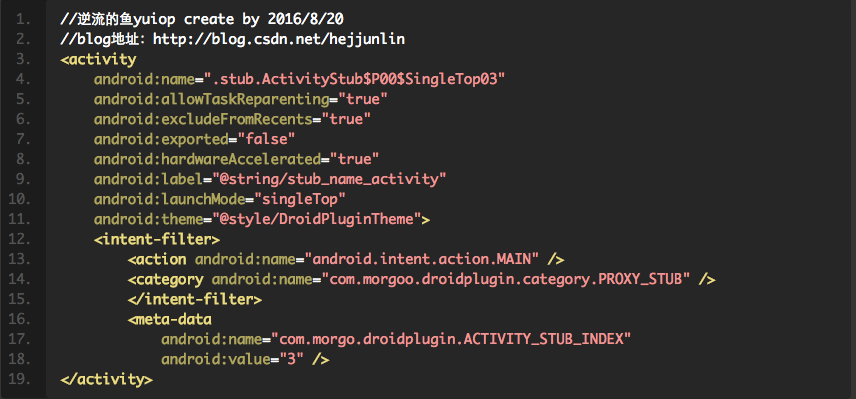 插件開發之360 DroidPlugin源碼分析(四)Activity預注冊占坑
插件開發之360 DroidPlugin源碼分析(四)Activity預注冊占坑
在了解系統的activity,service,broadcastReceiver的啟動過程後,今天將分析下360 DroidPlugin是如何預注冊占坑的?本篇文章主要分
 Android應用內社區SDK技術架構淺析
Android應用內社區SDK技術架構淺析
Android應用內社區SDK技術架構淺析應用內微社區是什麼 ? 圖1 圖2 雪球財經應用內社區 一、以友盟微社區為例簡單來說,友盟的微社區就是一款幫助
 andriod 在windows上環境配置
andriod 在windows上環境配置
andriod開發環境配置 個人信息:就讀於燕大本科軟件工程專業 目前大四; 本人博客:google搜索“cqs_2012”即可; 個人愛好:酷愛數據結構和算法,